代码随想录 | Day15 | 二叉树：递归遍历&&迭代遍历&&层序遍历

主要学习内容：

1.二叉树递归遍历

2.二叉树迭代遍历

3.二叉树层序遍历

递归三要素：

确定递归函数的参数和返回值： 确定哪些参数是递归的过程中需要处理的，那么就在递归函数里加上这个参数，并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
确定终止条件： 写完了递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。
确定单层递归的逻辑： 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。

来自代码随想录 (programmercarl.com)

144.二叉树的前序遍历

144. 二叉树的前序遍历 - 力扣（LeetCode）

递归遍历

按照递归三要素

1.确定递归函数的参数和返回值

由于我们是遍历所以不需要返回值，我们需要知道当前在二叉树的位置并且需要一个vector存放答案，所以参数就是二叉树结点和一个vector

2.确定终止条件

遍历到空指针就是到了叶子结点的下一结点，就算是这层递归函数的结束

3.确定单层循环的逻辑，由于是前序遍历所以我们按照中左右的顺序（前序中序后序说的就是中的所在的位置）

所以先处理本层结点，在将左孩子传入，后将右孩子传入即可

class Solution {
public:
    void tra(TreeNode * t,vector<int> &v)
    {
        if(t==nullptr)//终止条件
            return ;
        v.push_back(t->val);//中
        tra(t->left,v);//左
        tra(t->right,v);//右
    }
    vector<int> preorderTraversal(TreeNode* root) {
            vector<int> res;   
            tra(root,res);
            return res;
    }
};

迭代遍历

注意点：
1.先入栈右结点后入栈左结点，因为只有这样出现的时候才是先左后右的顺序

2.左右节点不为空的时候才会入栈

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
            vector<int> res;
            if(root==nullptr)
                return res;
            stack<TreeNode *> st;
            st.push(root);
            while(!st.empty())
            {
                TreeNode *t=st.top();
                res.push_back(t->val);
                st.pop();
                if(t->right)
                    st.push(t->right);
                if(t->left)
                    st.push(t->left);
            }
            return res;
    }
};

94.二叉树的中序遍历

94. 二叉树的中序遍历 - 力扣（LeetCode）

递归遍历

就是把中左右换成左中右剩下的都一模一样

class Solution {
public:
    void tra(TreeNode *t,vector<int> &v)
    {
        if(t==nullptr)
            return ;
        tra(t->left,v);
        v.push_back(t->val);
        tra(t->right,v);
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        tra(root,res);
        return res;
    }
};

迭代遍历

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) { // 指针来访问节点，访问到最底层
                st.push(cur); // 将访问的节点放进栈
                cur = cur->left;                // 左
            } else {
                cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
                st.pop();
                result.push_back(cur->val);     // 中
                cur = cur->right;               // 右
            }
        }
        return result;
    }
};

145.二叉树的后序遍历

145. 二叉树的后序遍历 - 力扣（LeetCode）

递归遍历

就是把中左右换成左中右剩下的都一模一样

class Solution {
public:
    void tra(TreeNode *t,vector<int> &v)
    {
        if(t==nullptr)
            return ;
        tra(t->left,v);
        tra(t->right,v);
        v.push_back(t->val);
    }
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        tra(root,res);
        return res;
    }
};

迭代遍历

相比前序的层序遍历，就是把左右结点的入栈顺序换了一下

后序遍历是左右中现在搞成了中右左，对没错，结束后把vector翻转一下就是答案

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        if(root==nullptr)
            return res;
        stack<TreeNode *> st;
        st.push(root);
        while(!st.empty())
        {
            TreeNode * t=st.top();
            res.push_back(t->val);
            st.pop();
            if(t->left)
                st.push(t->left);
            if(t->right)
                st.push(t->right);
        }
        reverse(res.begin(),res.end());
        return res;
    }
};

个人觉得主要掌握递归遍历即可，迭代遍历就只是照着敲了一遍

102.二叉树的层序遍历（BFS）

102. 二叉树的层序遍历 - 力扣（LeetCode）

所谓层序遍历就是按照一层一层的去遍历

使用队列这一个先入先出的数据结构，将结点入队

如动画所示使用for循环来遍历本层的所有节点并把他们的左右孩子都入队等待下一次层序遍历

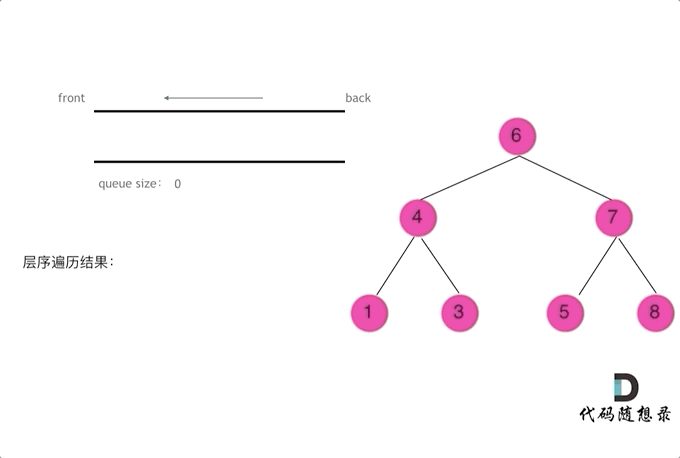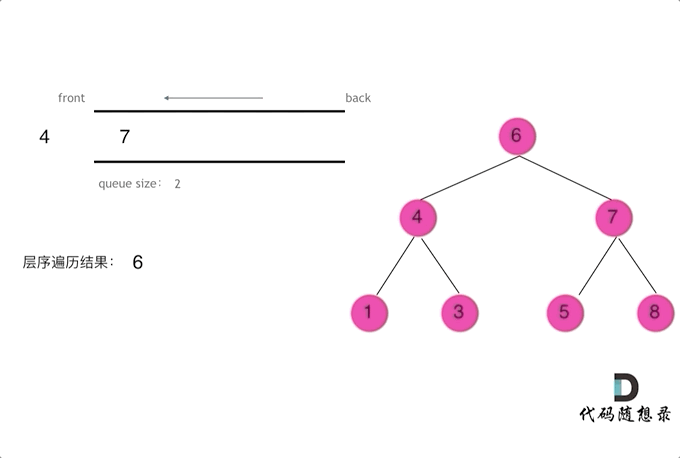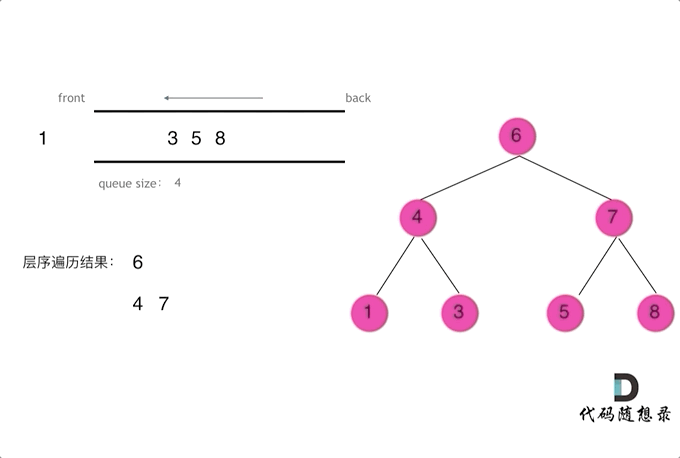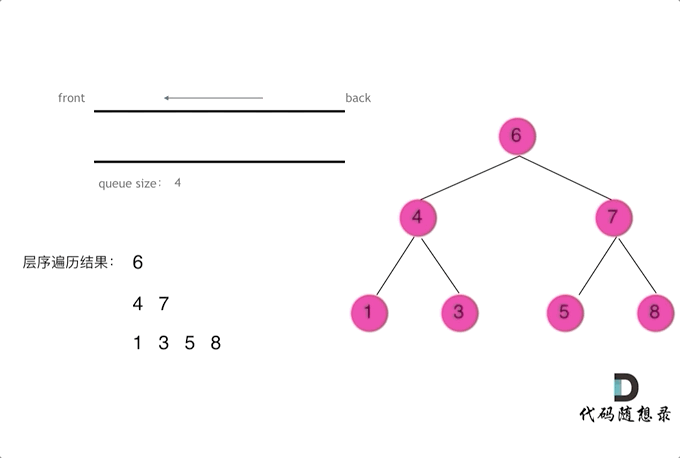
102二叉树的层序遍历

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode *> q;
        vector<vector<int>> res;
        if(root==nullptr)
            return res;
        q.push(root);
        while(!q.empty())
        {
            int size=q.size();
            vector<int> path;
            for(int i=0;i<size;i++)
            {
                TreeNode *t=q.front();
            q.pop();
            path.push_back(t->val);
            if(t->left)
                q.push(t->left);
            if(t->right)
                q.push(t->right);
            }
            res.push_back(path);
        }
        return res;
    }
};