代码随想录 | Day16 | 二叉树：翻转二叉树&&对称二叉树

主要学习内容：

1.二叉树的递归遍历

2.判断二叉树的递归遍历的方式是前中后那个非常重要

226.翻转二叉树

226. 翻转二叉树 - 力扣（LeetCode）

递归遍历

思路：

先想好递归三部曲里面的本层逻辑要干点什么，根据这个去想终止条件，返回值和函数参数会容易很多

本层逻辑中需要干的就是交换左右孩子就可以完成二叉树的翻转任务，我们只需要知道当前结点即可，所以函数参数需要传入当前节点。我们需要交换左右孩子，所以当前结点不可以为空，故终止条件为当前节点为空。我们只需要交换左右孩子，所以也不需要返回值。至此递归三部曲结束

1.确定函数参数和返回值

当前节点t以及void

1
void pre_tra(TreeNode *t)

2.确定终止条件

当前节点不为空

1
2
if(t==nullptr)
            return;

3.本层处理逻辑

交换左右孩子

1
swap(t->left,t->right);

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    void pre_tra(TreeNode *t)
    {
        if(t==nullptr)
            return;
        swap(t->left,t->right);
        pre_tra(t->left);
        pre_tra(t->right);
    }
    TreeNode* invertTree(TreeNode* root) {
        pre_tra(root);
        return root;
    }
};

注意点：遍历顺序

我在这里是选择了前序遍历，后序遍历是一样的，但是中序遍历会导致一些节点翻转两次导致相当于没有翻转

用以下代码可以避免这个问题，大家可以画图理解一下

1
2
3
4
5
6
7
8
void ino_tra(TreeNode *t)
    {
        if(t==nullptr)
            return;
        ino_tra(t->left);
    	swap(t->left,t->right);
        ino_tra(t->left);
    }

层序遍历

额就是老模板了，套用就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root==nullptr)
            return root;
        queue<TreeNode *> q;
        q.push(root);
        while(!q.empty())
        {
            int size=q.size();
            for(int i=0;i<size;i++)
            {
                TreeNode *t=q.front();
                q.pop();
                swap(t->left,t->right);
                if(t->left)
                    q.push(t->left);
                if(t->right)
                    q.push(t->right);
            }
        }
        return root;
    }
};

101.对称二叉树

101. 对称二叉树 - 力扣（LeetCode）

递归遍历

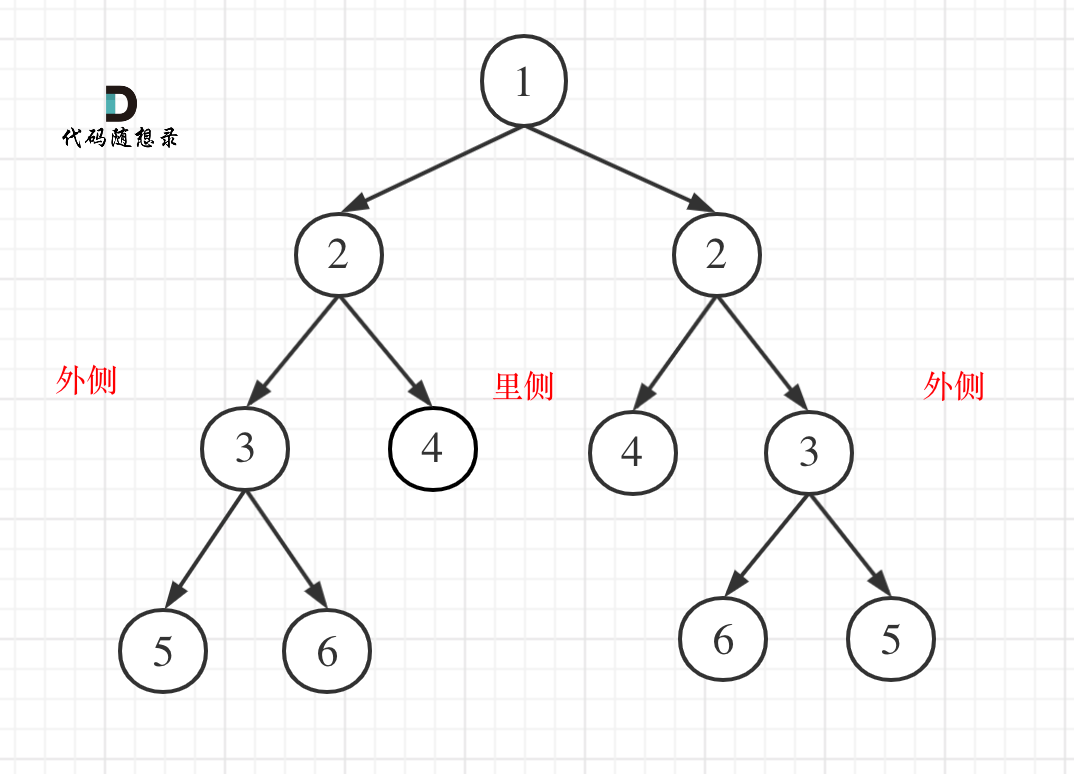
20210203144624414

我们需要判断是不是对称二叉树，需要同时遍历左右子树来看两者是否相同才可以，所以要同时遍历两棵子树

我们需要判断遍历的两颗子树是否相同，并且要返回结果来对上层结点进行判断，所以需要使用后序遍历才行，也

只能使用后序遍历

1.确定参数和返回值

要判断是否相同，返回值毫无疑问是bool，我们要同时判断两个子树，也就是需要两个子树的结点，也就是函数参数是两个子树结点

1
bool cmp(TreeNode *l,TreeNode *r)

2.确定终止条件

1
2
3
4
5
6
7
8
9
10
11
		if(l==nullptr&&r==nullptr)//两者均为空
            return true;
		//其中一个不为空
        else if(l!=nullptr&&r==nullptr)
            return false;
        else if(l==nullptr&&r!=nullptr)
            return false;
		//均不空但是值不相同
        else if(l->val!=r->val)
            return false;
//最后只剩下均不为空且值相同的情况

3.本层处理逻辑

1
2
3
bool left=cmp(l->left,r->right);
bool right=cmp(l->right,r->left);
return left&&right;

见上图，判断是否翻转判断是外侧和内侧是否相等，即左边的左子树和右边的右子树比较，右边的左子树和左边的左子树进行比较

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    bool cmp(TreeNode *l,TreeNode *r)
    {
        if(l==nullptr&&r==nullptr)
            return true;
        else if(l!=nullptr&&r==nullptr)
            return false;
        else if(l==nullptr&&r!=nullptr)
            return false;
        else if(l->val!=r->val)
            return false;
        bool left=cmp(l->left,r->right);
        bool right=cmp(l->right,r->left);
        return left&&right;
        //可以简写为
        //return cmp(l->left,r->right)&&right=cmp(l->right,r->left);
    }
    bool isSymmetric(TreeNode* root) {
        if(root==nullptr)
            return true;
        return cmp(root->left,root->right);
    }
};

使用队列进行遍历（这不是层序遍历）

思路：

不多说了看图吧

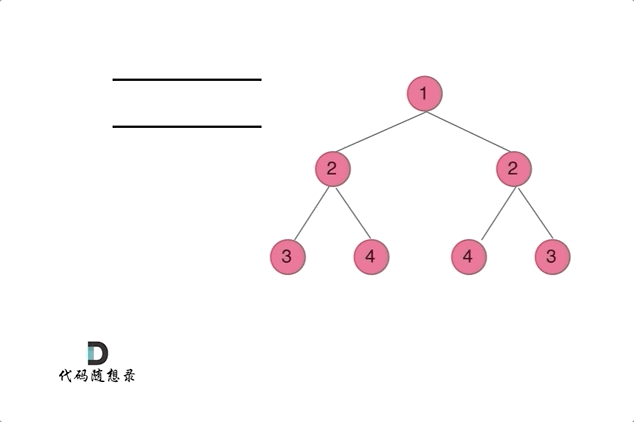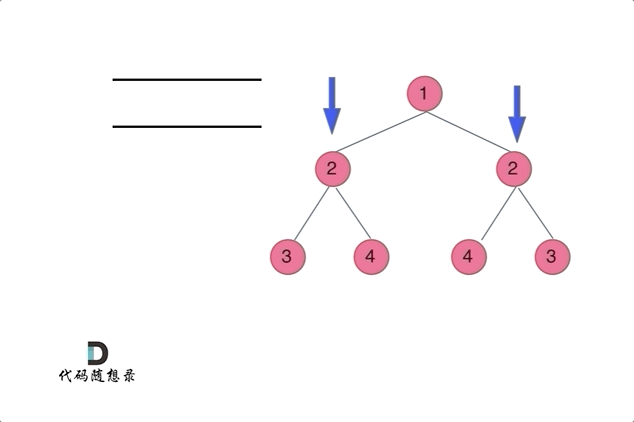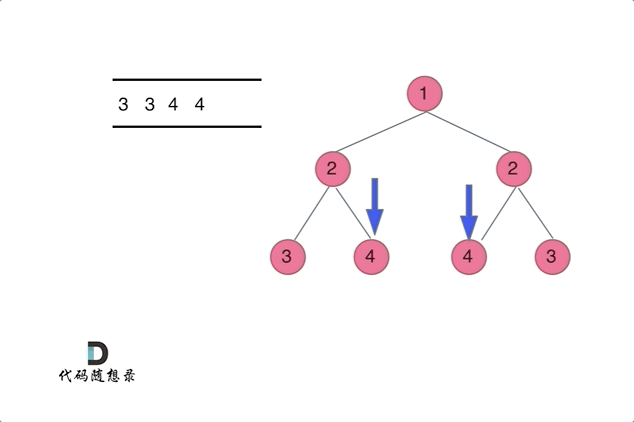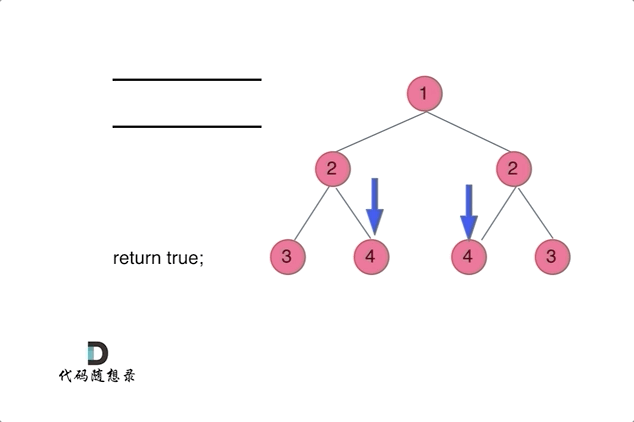
101.对称二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        queue<TreeNode *> q;
        if(root==nullptr)
            return true;
        q.push(root->left);
        q.push(root->right);
        while(!q.empty())
        {
            TreeNode *left=q.front();
            q.pop();
            TreeNode *right=q.front();
            q.pop();
            //两者都为空 对称 继续遍历
            if(!left&&!right)
                continue;
            //一个为空一个不为空或者两者值不同 则不对称
            if(!right||!left||right->val!=left->val)
                return false;
            //入队孩子节点 注意入队的顺序要按照从两边向中间的顺序入队
            q.push(left->left);
            q.push(right->right);
            q.push(left->right);
            q.push(right->left);
        }
        //出来了说明就是对称的
        return true;
    }
};

自己写的

也是有很多问题

基本思路是层序遍历把值都收集到一个数组，如果为空的话就放进数组一个特殊值，然后遍历这个数组看这个数组对称与否

很明显的问题是，当节点的值和数组特殊值一样的时候就G了（虽然能过但是大家还是学习前面两个方法吧）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
//自己写的
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        queue<TreeNode *> q;
        int n=0;
        if(root==nullptr)
            return true;
        q.push(root);
        while(!q.empty())
        {
            int size=q.size();
            vector<int> path;
            n++;
            for(int i=0;i<size;i++)
            {
                TreeNode *t=q.front();
                q.pop();
                if(t->left)
                {
                    q.push(t->left);
                    path.push_back(t->left->val);
                }
                else
                    path.push_back(0x3f3f3f3f);
                if(t->right)
                {
                     q.push(t->right);
                     path.push_back(t->right->val);
                }
                else
                    path.push_back(0x3f3f3f3f);
            }
            if(path.size()%2!=0)
                return false;
            for(int i=0;i<path.size()/2;i++)
            {
                if(path[i]!=path[path.size()-i-1])
                    return false;
            }
        }
        return true;
    }
};

还是多写写这道题吧，思路不太好想