代码随想录 | Day25 | 二叉树：从中序与后序遍历构造二叉树&&最大二叉树

主要学习内容：
用中序和后序来构建二叉树

106.从中序与后序遍历构造二叉树

106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

解法思路：

先想想如果没有这个图的话，我们会如何把根据这两个数组把树画出来。

1.中序是左中右，后序是左右中，说明后序数组的末尾肯定是当前还没构造的部分的根结点

2.接下来再根据这个值去中序里面找，找到的话，那它的前面就是左子树，后面就是右子树

3.根据中序数组左子树结点数量，可以确定后序数组中左右的分界，这样就找到了中序和后序数组中，左子树和右子树的范围

4.也就是分别找到了左子树和右子树他们自己的中序和后序数组

5.递归左子树和右子树的中序后序数组，建立左右子树，知道整棵树构建完毕

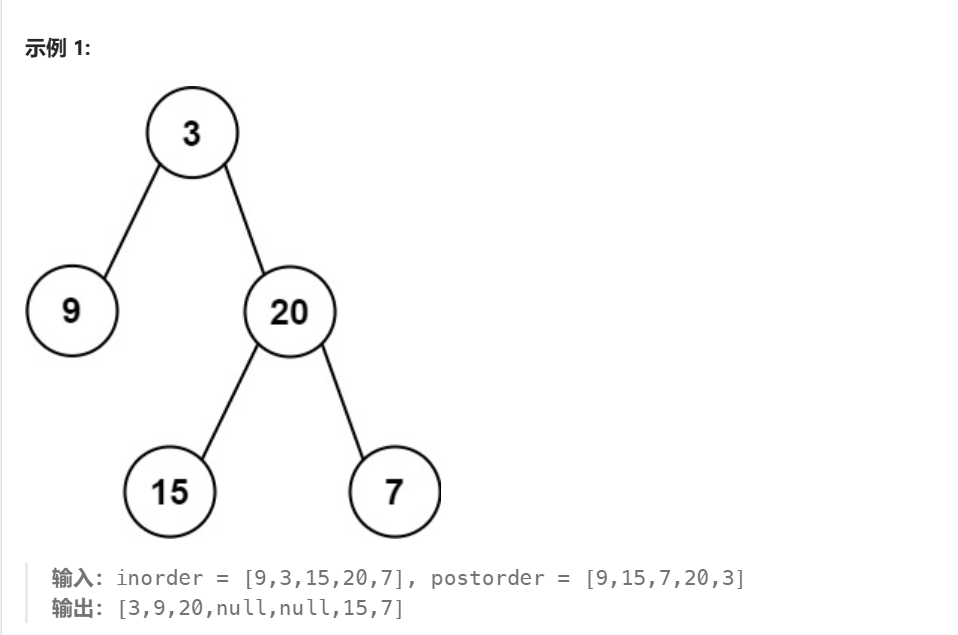
比如下面，这张图的构造过程

1.先找到根结点3

2.3前面是左子树9，后面是右子树15,20,7

3.左子树大小为1说明，后序数组前面1个数是左子树，到末尾的根结点前是右子树15,7,20

4.左子树中序 ：9 后序：9

右子树中序 ：15 20 7 后序：15 7 20

5.递归9和9 15 20 7和15 7 20

image-20240927152225450

现在我们了解了大致过程，难点在于

1.我们该如何知道构造完的根结点在哪，即我们的递归函数返回值是什么？

2.递归函数的终止条件又该是什么？

1.我们需要最后返回我们构造的二叉树，所以我们的返回值得是我们构造二叉树的根结点，也是通过函数返回值得到根节点

2.终止条件应该是后序数组为空，后序数组为空说明已经没有结点需要进行构造了、

1.函数参数和返回值

1
TreeNode *tra(vector<int> i, vector<int> p)

i，p对应当前构造子树的中序和后序数组，返回值TreeNode * 是我们的根结点

2.终止条件

1
if(p.size()==0) return nullptr;

后序数组为空

3.本层代码逻辑

这部分是最难的地方，我们需要把我们刚刚想象的过程用代码进行复刻、

1.找到当前子树的根结点，就是后序数组的最后一个值

1
TreeNode *t=new TreeNode(p[p.size()-1]);

2.找到中序数组中左子树和右子树的切分点，即在中序数组中找到根节点，找到根节点的下标位置以后就break

1
2
3
4
int index=0;
for(index=0;index<i.size();index++)
	if(i[index]==t->val)
		break;

3.构造左子树，要注意采用的区间是左闭右闭还是左闭右开，不管用哪种都要统一

我采用的是左闭右开，因为迭代器的begin和end是左闭右开的

我们切割左子树的中序和后序

中序就是从开始到根结点的下标值，[0,index)

后序也是[0,index)

1
2
3
t->left=tra(
    vector<int>(i.begin(),i.begin()+index),
    vector<int>(p.begin(),p.begin()+index));

4.构造右子树

我们切割右子树的中序和后序

中序就是从开始到根结点的下标值，[index+1,end)，end是只想末尾位置的下一位置的迭代器（可以理解为指针），index+1是因为要把根结点跳过，他不属于子树内容

后序是[index,end-1)，因为后序的左右子树直接挨着，而最后一个是根节点，我们一样不要根结点

5.返回根结点

1
return t;

本层逻辑完整代码：

1
2
3
4
5
6
7
8
TreeNode *t=new TreeNode(p[p.size()-1]);
      int index=0;
      for(index=0;index<i.size();index++)
          if(i[index]==t->val)
              break;
      t->left=tra(vector<int>(i.begin(),i.begin()+index),vector<int>(p.begin(),p.begin()+index));
      t->right=tra(vector<int>(i.begin()+index+1,i.end()),vector<int>(p.begin()+index,p.end()-1));
      return t;

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    TreeNode *tra(vector<int> i, vector<int> p)
    {
        if(p.size()==0) return nullptr;
        TreeNode *t=new TreeNode(p[p.size()-1]);
        int index=0;
        for(index=0;index<i.size();index++)
            if(i[index]==t->val)
                break;
        t->left=tra(vector<int>(i.begin(),i.begin()+index),vector<int>(p.begin(),p.begin()+index));
        t->right=tra(vector<int>(i.begin()+index+1,i.end()),vector<int>(p.begin()+index,p.end()-1));
        return t;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return tra(inorder,postorder);
    }
};

654.最大二叉树

654. 最大二叉树 - 力扣（LeetCode）

解法：

这没啥好说的，就和上一题一模一样，就是从后序找根节点换成找一个数组里面的最大值了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    TreeNode *tra(vector<int> nums)
    {
        //终止条件
        if(nums.size()==0)
            return nullptr;
        //记录最大值下标和最大值
        int index=0,maxVal=INT_MIN;
        for(int i=0;i<nums.size();i++)
            if(nums[i]>maxVal)
            {
                maxVal=nums[i];
                index=i;
            }
        //构建根节点
        TreeNode *t=new TreeNode(maxVal);
        //构建左子树，还是采用左闭右开
        t->left=tra(vector<int>(nums.begin(),nums.begin()+index));
        //构建右子树
        t->right=tra(vector<int>(nums.begin()+index+1,nums.end()));
        //返回根节点
        return t;
    }
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return tra(nums);
    }
};