Day30 | 回溯算法 组合总和II&&切割问题

代码随想录 | Day30 | 回溯算法：组合总和II&&切割问题

主要学习内容：

树枝树层去重以及切割问题解法，模板总结

40.组合总和II

40. 组合总和 II - 力扣（LeetCode）

解法思路：

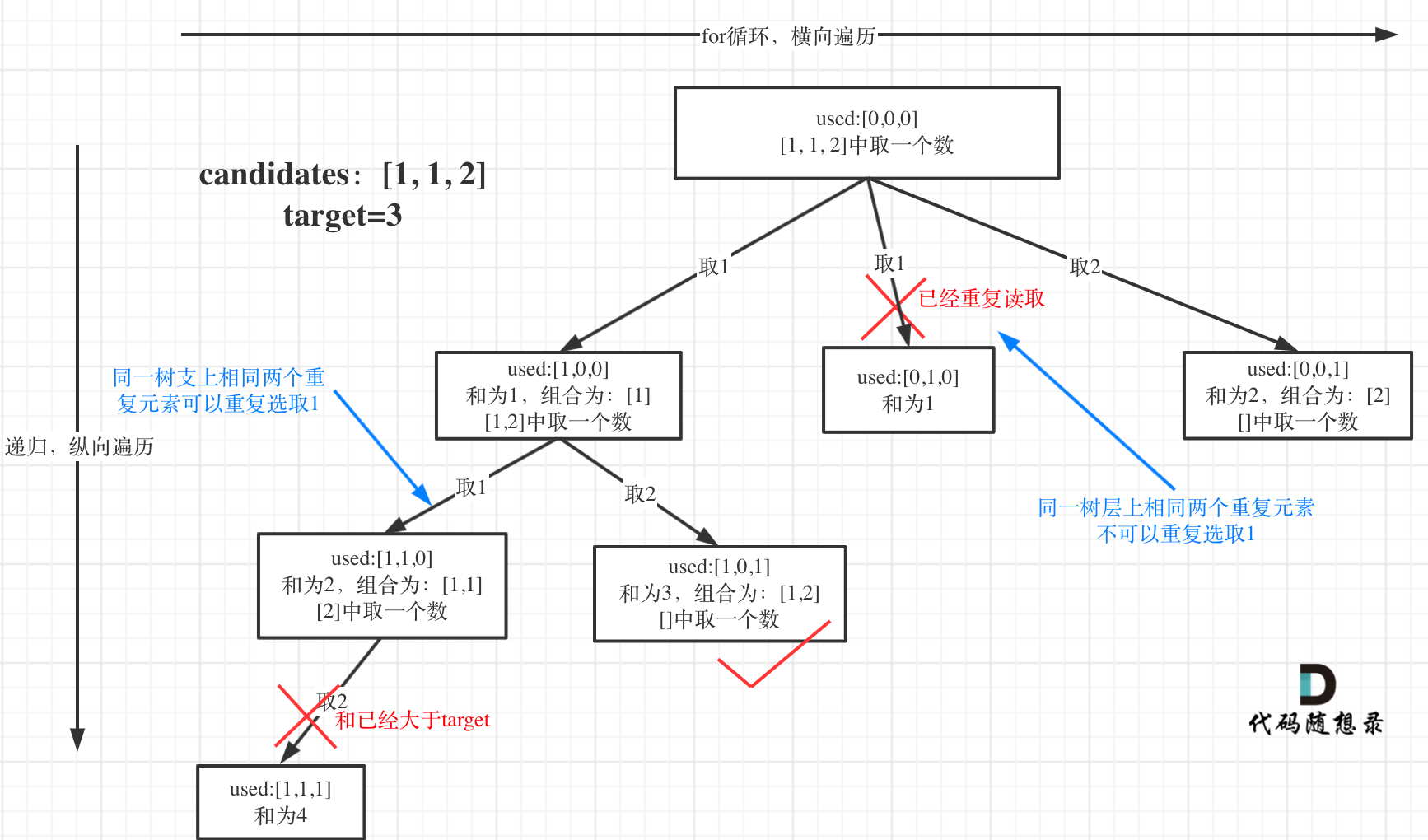
这个是数层间去重，不是树枝去重，即如图所示这样

树枝去重我们传入的参数index赋值为i+1而不是i就已经防止了树枝去重，而在树层去重，是在同一层不能选重复的，我们之前说过，一个for循环可以产生一层的结点。现在要在同一层不能选重复的，那说明，在for循环里面选择过的数（比如在i=0时压入了path），在本层函数的for循环其他时候不能压入path。

1.函数参数和返回值

vector<vector<int>> res;
void backtracking(vector<int> path,int sum,int index,vector<int> candidates,int target)

res存放结果

path存放目前放入的数

sum为当前的和

index为开始的结点，从index开始循环

candidates和target都是题目给的

2.终止条件

大于target返回

等于target收集答案返回

if(sum>target)
	return;
if(sum==target)
{
	res.push_back(path);
	return;
}

3.本层代码逻辑

used作为一个哈希表，一个数要是被选过了那就是false，只要是false，在数的同层即在for循环里面不能被选（表现为第一个节点选了1第二个不能选1），但是它的下层递归函数，即树枝之间可以重复选（表现为选1下面的子节点还可以选），因为每层递归函数的used都不一样的，到新的一层，它的used是全true的

vector<bool> used(candidates.size(),true); 
for(int i=index;i<candidates.size();i++)
{
    //只有没被选过才可以选，选过了就直接跳过
	if(used[candidates[i]])
	{
		path.push_back(candidates[i]);
		used[candidates[i]]=false;
		backtracking(path,sum+candidates[i],i+1,candidates,target);
		path.pop_back();
	}
}

要注意candidates一定要是排过序的。不然会出现

这样的情况，即有1,2,5还有2,1,5这种的

完整代码：

class Solution {
public:
    vector<vector<int>> res;
    void backtracking(vector<int> path,int sum,int index,vector<int> candidates,int target)
    {
        if(sum>target)
            return;
        if(sum==target)
        {
            res.push_back(path);
            return;
        }
        vector<bool> used(candidates.size(),true); 
        for(int i=index;i<candidates.size();i++)
        {
            if(used[candidates[i]])
            {
                path.push_back(candidates[i]);
                used[candidates[i]]=false;
                backtracking(path,sum+candidates[i],i+1,candidates,target);
                path.pop_back();
            }
        }
    }
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<int> path;
        vector<bool> used(candidates.size(),true);
        sort(candidates.begin(),candidates.end());
        backtracking(path,0,0,candidates,target);
        return res;
    }
};

再看代码随想录的去重逻辑

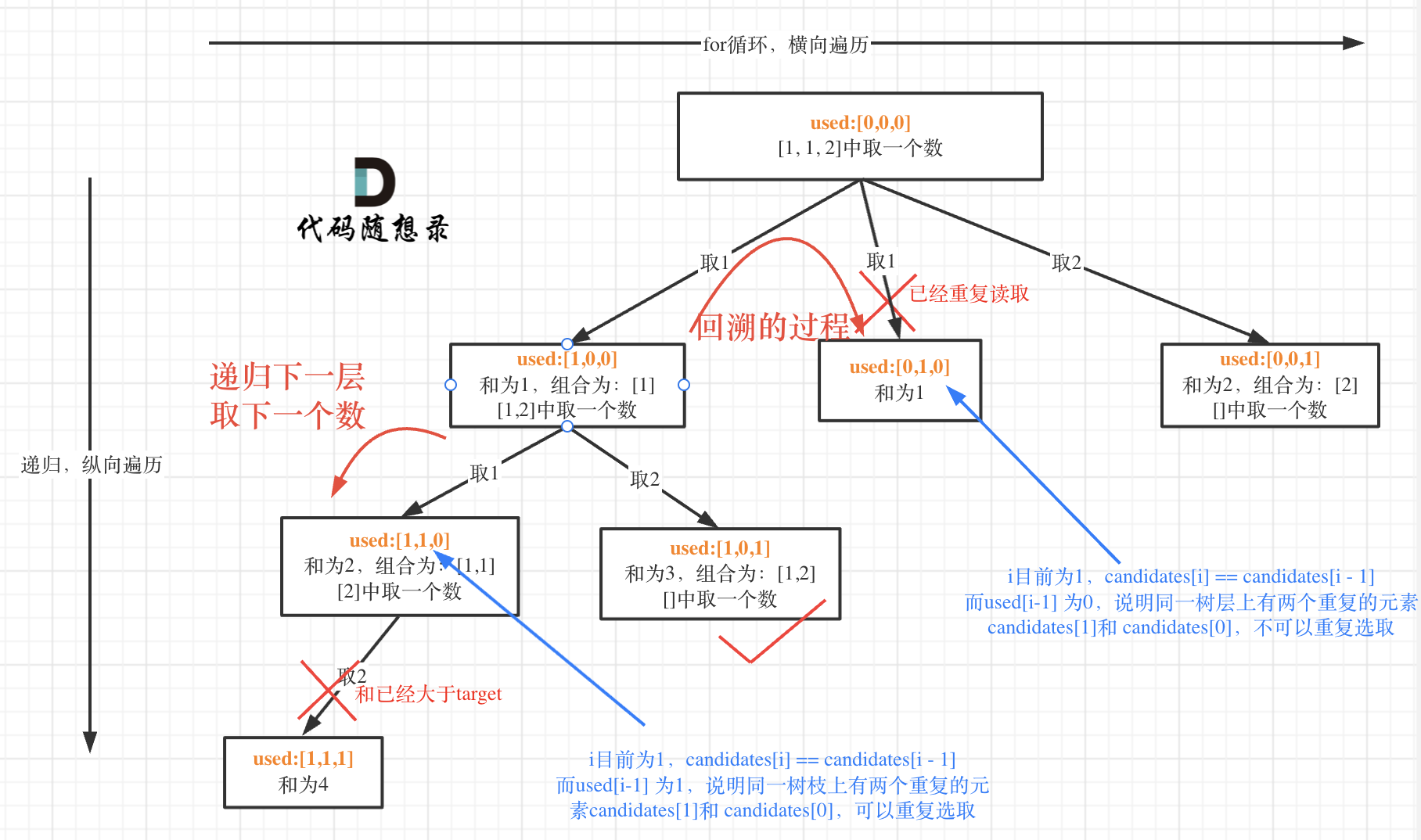
这个是连带used一起回溯，如果是true说明在上层递归函数里面用过，这个无所谓，因为树枝之间是可以重复的（注意，这个重复不是它本身，它本身的重复我们传入的i+1参数已经排除掉了）

如果i和i-1是同一个数，并且used是false说明是同一层的，并且i-1那个数已经作为结点被选过了，那么i这个数就不需要再来一遍了，直接continue

那么单层搜索的逻辑代码如下：

for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
    // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
    // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
    // 要对同一树层使用过的元素进行跳过
    if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
        continue;
    }
    sum += candidates[i];
    path.push_back(candidates[i]);
    used[i] = true;
    backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1：这里是i+1，每个数字在每个组合中只能使用一次
    used[i] = false;
    sum -= candidates[i];
    path.pop_back();
}

个人觉得还是我的好理解一点

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {
        if (sum == target) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
            // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
            // 要对同一树层使用过的元素进行跳过
            if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
                continue;
            }
            sum += candidates[i];
            path.push_back(candidates[i]);
            used[i] = true;
            backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1，这里是i+1，每个数字在每个组合中只能使用一次
            used[i] = false;
            sum -= candidates[i];
            path.pop_back();
        }
    }

public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<bool> used(candidates.size(), false);
        path.clear();
        result.clear();
        // 首先把给candidates排序，让其相同的元素都挨在一起。
        sort(candidates.begin(), candidates.end());
        backtracking(candidates, target, 0, 0, used);
        return result;
    }
};

切割问题

131.分割回文串

131. 分割回文串 - 力扣（LeetCode）

思路：

难点：

1..在递归函数的for循环中如何切割子串并判断是不是回文串？

2.如果遇到了错误的集合，即收集到一半，另外一半怎么分割都不会是回文串，那是如何避免把这个path放入答案res中的呢？

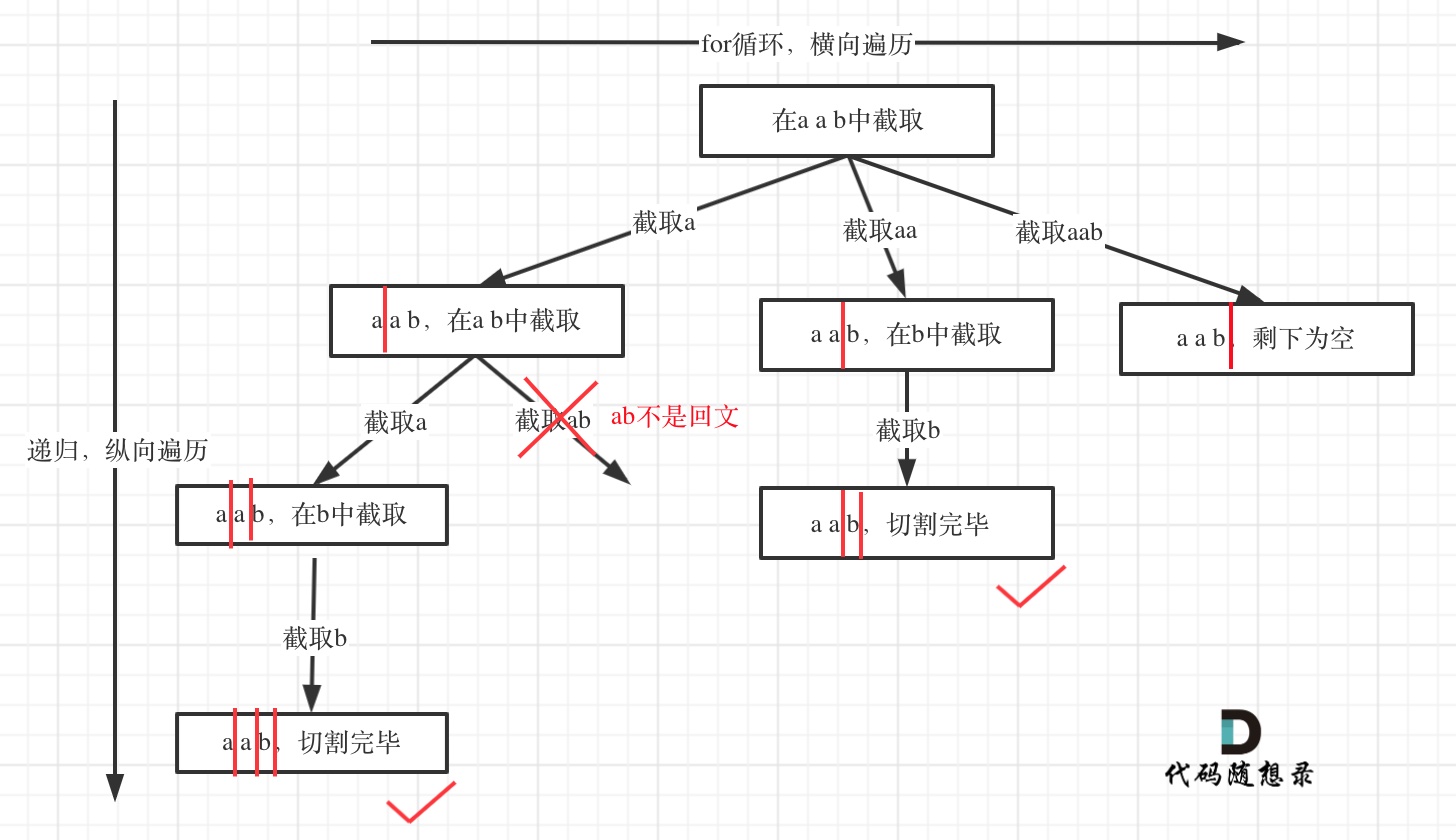
for循环是控制树的深度

切割问题和组合问题是同一类问题，都是在叶子结点收获答案。比如[1,2,3,4]中任意两个数字的组合，它的二叉树第一层是分别以1,2,3,4这四个数为根结点的子树，然后往下延伸

而这道题是，切割1,2,34看看是不是回文的，在原来2的地方我们要存放和判断的是[1,2]这个区间，看看他俩是不是回文的，在3的地方是[1,2,3]要看看这三个数是不是回文的

如果[1,2]是回文的，那切割线就到了2后面，在下层的递归函数里面去看3,4有没有切割成回文串的方案

以前是只要push一个元素进去就完事了，现在是要看前面整个区间是否符合条件，怎么在for循环中把这个区间表示出来并且判断是不是回文串，是主要的难点（第一个难点）。

1.函数返回值和参数

vector<vector<string>> res;
void backtracking(string s,vector<string> path,int index)

res记录结果

path收集当前分割集

index充当切割线，是切割线所在的位置

2.终止条件

只有当切割线到达字符串末尾，才算是结束。

if(index>=s.size())
{
	res.push_back(path);
	return;
}

3.本层逻辑

判断是不是回文串

bool is(string s,int begin,int end)
   {
       for(int i=begin,j=end;i<j;i++,j--)
       {
           if(s[i]!=s[j])
               return false;
       }
       return true;
   }

首先要充分理解[index,i]这个区间，就是前面所说的在组合中相当于是[1,2]，[1,2,3]这类的结点，可以以区间的形式判断是不是回文串，如果是的话就放入path，不是的话直接把这个子树砍掉，即不让他进入下层的循环，因为不管后半部分怎么切割，前半部分已经不是回文串了。

去到下层函数之后，就已经是从切割线以后，即i+1处开始进行搜索了，然后重复判断是不是回文串，是的话才会放入path。

如果到了某一层发现不是回文串，会一直向上返回，然后被pop出来。

有一个不是回文串，就不会被放入res，因为它那一层的递归函数的index不会到达s.size()

index<=i<s.size()
结束条件的index>=s.size()的情况是当上层的i=s.size()时给下层传i+1结束的

for(int i=index;i<s.size();i++)
 {
     if(is(s,index,i))
         path.push_back(string(s.begin()+index,s.begin()+i+1));
     else
         continue;
     backtracking(s,path,i+1);
     path.pop_back();
 }

完整代码：

class Solution {
public:
    bool is(string s,int begin,int end)
    {
        for(int i=begin,j=end;i<j;i++,j--)
        {
            if(s[i]!=s[j])
                return false;
        }
        return true;
    }
    vector<vector<string>> res;
    void backtracking(string s,vector<string> path,int index)
    {
        if(index>=s.size())
        {
            res.push_back(path);
            return;
        }
       for(int i=index;i<s.size();i++)
        {
            if(is(s,index,i))
                path.push_back(string(s.begin()+index,s.begin()+i+1));
            else
                continue;
            backtracking(s,path,i+1);
            path.pop_back();
        }
    }
    vector<vector<string>> partition(string s) {
        vector<string> path;
        backtracking(s,path,0);
        return res;
    }   
};

93.复原IP地址

93. 复原 IP 地址 - 力扣（LeetCode）

思路:

和上一题一模一样思路，就是把is函数换成判断数字是否大于255即可

1.函数返回值和参数

vector<string> res;
void backtracking(string path,int index,string s,int k)

res记录结果

path收集当前分割集

index充当切割线，是切割线所在的位置

k是记录分了几段了，4段以后就判断是否要收集结果

2.终止条件

k==4//已经分了4段了

index>=s.size()//代表切割线已经到达了字符串末尾

都满足则收集结果，没到末尾那肯定不是结果，就return

if(k==4)
{
	if(index>=s.size())
	{
		path.pop_back();
		res.push_back(path);
	}
	return;
}

3.本层逻辑

判断是不是每一段ip是否合法

1.大于255肯定是错的

2.只有一位（主要解决单0问题）肯定是对的

3.不大于255，不止有一位，开头还是0，肯定是错的

4.上面没返回false，那肯定是true

bool is(string s,int begin,int end)
{
	string str(s.begin()+begin,s.begin()+end);
	if(stoi(str)>255)
		return false;
	if(str.size()==1)
		return true;
	if(str[0]=='0')
		return false;
	return true;
}

和上一题一样，也是采用[index,i]的区间对ip地址进行切割，index为切割线，对[index,i]这一段进行合法性判断，合法的话就进入下一层递归

注意上一题是continue，是因为后面还有可能有别的方案可以切割，而这个如果一旦判断不合法，那后面的就不用继续了，所以是break。举个例子，这一段已经是300了，那后面不管加上哪个数字，那都是比300大的数，更不可能合法了。

for(int i=index;i<s.size();i++)
{
	string str(s.begin()+index,s.begin()+i+1);
	if(is(s,index,i+1))
		path=path+str+".";
	else
		break;
	backtracking(path,i+1,s,k+1);
	path=string(path.begin(),path.end()-1-str.size());
}

完整代码：

class Solution {
public:
    vector<string> res;
    bool is(string s,int begin,int end)
    {
        string str(s.begin()+begin,s.begin()+end);
        if(str.size()==1)
            return true;
        if(str[0]=='0')
            return false;
        if(stoi(str)>255)
            return false;
        return true;
    }
    void backtracking(string path,int index,string s,int k)
    {
        if(k==4)
        {
            if(index>=s.size())
            {
                path.pop_back();
                res.push_back(path);
            }
            return;
        }
        for(int i=index;i<s.size();i++)
        {
            string str(s.begin()+index,s.begin()+i+1);
            if(is(s,index,i+1))
                path=path+str+".";
            else
                break;
            backtracking(path,i+1,s,k+1);
            path=string(path.begin(),path.end()-1-str.size());
        }
    }
    vector<string> restoreIpAddresses(string s) {
        string path;
        backtracking(path,0,s,0);
        return res;
    }
};

切割问题模板

res结果集;
bool is([index,i]区间)
{
    //判断合法性
    return true or false;
}
void backtracking(函数参数)
{
    if(终止条件)
    {
        res结果收集;
	}
    for(int i=index;i<s.size();i++)
    {
        if(is(传入[index,i]这个区间))
            path收集;
        else
            break or continue;
        //下一层递归
        backtracking(函数参数);
        回溯过程;
    }
}