Day33 | 回溯算法 棋盘问题

代码随想录 | Day33 | 回溯算法：棋盘问题

主要学习内容：

1.棋盘问题就和组合问题差不多

2.多维的回溯就和一维的思路想法差不多，只是遍历方式不同

51.N皇后

51. N 皇后 - 力扣（LeetCode）

解法思路：

遍历思路

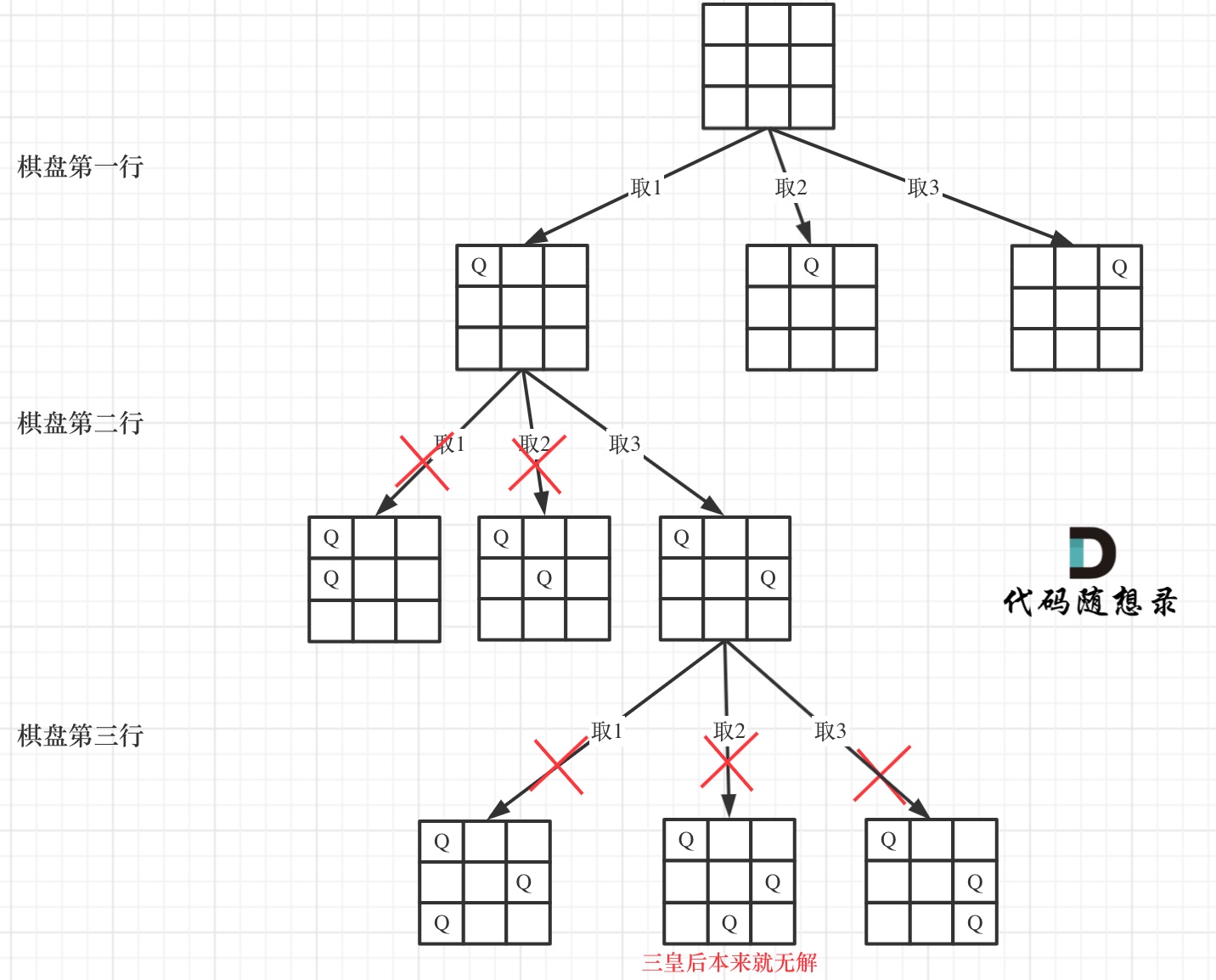
如下图所示，我们在树的每一层按照列遍历，因为在上一层的列（比如第4列）放过的，在这一层的前面的列还是有可能放皇后（4之前的第1,2,列），所以我们应该在每一层都从0开始遍历

通过传入的参数i控制该第几行了

合法性判断

如果同一行同一列同一斜线放过的话就不能放了，因为我们通过i控制行，树的每层本身也就只会放一个，所以同一行不用查，只用查同一列和斜线。

1.函数参数和返回值

vector<vector<string>> res;
void backtracking(vector<string> path,int i,int n)

res存放结果

path存放目前的棋盘

i控制该第几行了

n传入一共有几行几列作为终止条件使用

2.终止条件

我们的i是下标，从0开始，所以等于n的时候就是已经收集了n行，这就是结果

if(i==n)
{
	res.push_back(path);
	return;
}

3.本层代码逻辑

j代表列下标

通过is函数判断i，j位置合法性，合法就放入皇后Q，然后进入下一层循环，那就是传入下一行即i+1

不合法就跳过本次循环

for(int j=0;j<n;j++)
{
	if(is(path,i,j,n))
	{
		path[i][j]='Q';
		backtracking(path,i+1,n);
		path[i][j]='.';
	}
}

合法性判断：

同一行不用判断

同一斜线只用判断之前的不用判断之后的

bool is(vector<string> path,int c,int r,int n)
   {
       //同一列
       for(int i=0;i<c;i++)
           if(path[i][r]=='Q')
               return false;
      	//左上斜线
       for(int i=c-1,j=r-1;i>=0&&j>=0;i--,j--)
       {
           if(path[i][j]=='Q')
               return false;
       }
       //右上斜线
       for(int i=c-1,j=r+1;i>=0&&j<n;i--,j++)
       {
           if(path[i][j]=='Q')
               return false;
       }
       return true;
   }

完整代码：

class Solution {
public:
    vector<vector<string>> res;
    bool is(vector<string> path,int c,int r,int n)
    {
        for(int i=0;i<c;i++)
            if(path[i][r]=='Q')
                return false;
        for(int i=c-1,j=r-1;i>=0&&j>=0;i--,j--)
        {
            if(path[i][j]=='Q')
                return false;
        }
        for(int i=c-1,j=r+1;i>=0&&j<n;i--,j++)
        {
            if(path[i][j]=='Q')
                return false;
        }
        return true;
    }
    void backtracking(vector<string> path,int i,int n)
    {
        if(i==n)
        {
            res.push_back(path);
            return;
        }
        for(int j=0;j<n;j++)
        {
            if(is(path,i,j,n))
            {
                path[i][j]='Q';
                backtracking(path,i+1,n);
                path[i][j]='.';
            }
        }
    }
    vector<vector<string>> solveNQueens(int n) {
        vector<string> path(n,string(n,'.'));
        backtracking(path,0,n);
        return res;
    }
};

37.解数独II

37. 解数独 - 力扣（LeetCode）

思路：

还是和之前一样的思路，就是树形结构，然后每层节点由for循环产生，这次产生的数要在1-9里面挑选符合条件的数字罢了

难理解的点

1.为什么非得用二维而不是一维

和N皇后不同，N皇后是这一行选完一个就到了下一行

解数独是这一行的这个选完了，还得在这一行继续选下一个

2.之前遍历的是一维数组，现在要遍历二维数组

其实也还好说，就把它按照一维数组的方式来写，想象一下二维数组给铺平，其实还是一个一维数组，只是在代码形式上遍历的时候按照二维方式遍历就完事

3.明明上面都理解了也写出来了，但是超时了或者栈溢出了

这个留着下面说吧

1.函数参数和返回值

vector<vector<string>> res;
bool backtracking(vector<vector<char>>& board,int n)

res存放结果

n是棋盘的边长

2.终止条件

本题没有终止条件

3.本层代码逻辑

先看看第一个版本

void返回值的，这种的没有剪枝操作，就是把所有的情况遍历一遍，这种复杂度是最大的，毫不意外的超时了

多计算的是哪一部分呢？

假如我们在第2行第2列的位置发现，这个位置填了9个数，全都行不通，那就没必要填剩下的7行了，说明是上面填的数错了，我们应该往回返，去修改上面的数字，而void会继续往下遍历，填完这7行并输出结果，可能导致最后的结果也是错的

void backtracking(vector<vector<char>>& board,int n)
   {
       for(int i=0;i<n;i++)
           for(int j=0;j<n;j++)
           {
               for(char k='1';k<='9';k++)
               {
                   if(is(board,i,j,k,n))
                   {
                       board[i][j]=k;
                       backtracking(board,n);
                       board[i][j]='.';
                   }
               }
           }
   }
bool is(vector<vector<char>>& board,int r,int c,char k,int n)
   {
       if(board[r][c]!='.')
           return false;
       //检查行 有没有重复
       for(int i=0;i<n;i++)
           if(board[r][i]==k)
               return false;
       //检查列
       for(int i=0;i<n;i++)
           if(board[i][c]==k)
               return false;
       //所处3*3宫内的第一个元素行下标
       int row=(r/3)*3;
       //列
       int col=(c/3)*3;
       for(int i=row;i<row+3;i++)
           for(int j=col;j<col+3;j++)
               if(board[i][j]==k)
                   return false;
       return true;
   }

再看看第二个版本

bool作为返回值，能找到一个合理的方案返回true，找不到就返回false

最后出了循环说明找到了返回true

加上了剪枝操作，就避免了上面那样的超时问题

当在当前空格无法填入任何有效数字时（即内层循环结束后没有返回true），它会立即返回false给上一层递归。这样，上一层递归就知道当前分支无法成功，并且会停止尝试在当前空格填入其他数字，而是回溯到上一个空格并尝试下一个数字。此外，当整个数独板被成功填充时，它会返回true，表示找到了一个解决方案。

还要注意，我们只有是’.’的时候才会进行赋值。

bool backtracking(vector<vector<char>>& board,int n)
   {
       for(int i=0;i<n;i++)
           for(int j=0;j<n;j++)
           {
               if(board[i][j]=='.')
               {
                   for(char k='1';k<='9';k++)
               	{
                       if(is(board,i,j,k,n))
                       {
                           board[i][j]=k;
                           if(backtracking(board,n)) return true;
                           board[i][j]='.';
                       }
               }
               return false;
			}
           }
       return true;
   }

完整代码：

class Solution {
public:
    vector<vector<char>> res;
    bool is(vector<vector<char>>& board,int r,int c,char k,int n)
    {
        //检查行 有没有重复
        for(int i=0;i<n;i++)
            if(board[r][i]==k)
                return false;
        //检查列
        for(int i=0;i<n;i++)
            if(board[i][c]==k)
                return false;
        //所处3*3宫内的第一个元素行下标
        int row=(r/3)*3;
        //列
        int col=(c/3)*3;
        for(int i=row;i<row+3;i++)
            for(int j=col;j<col+3;j++)
                if(board[i][j]==k)
                    return false;
        return true;
    }
    bool backtracking(vector<vector<char>>& board,int n)
    {
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
            {
                if(board[i][j]=='.')
                {
                    for(char k='1';k<='9';k++)
                	{
                        if(is(board,i,j,k,n))
                        {
                            board[i][j]=k;
                            if(backtracking(board,n)) return true;
                            board[i][j]='.';
                        }
                }
                return false;
				}
            }
        return true;
    }
    void solveSudoku(vector<vector<char>>& board) {
        int n=board.size();
        bool l=backtracking(board,n);
        return;
    }
};