01背包模板
01背包是
动态规划应该如何学习?-CSDN博客中的选或不选情况
完全背包模板总结-CSDN博客
选或不选
灵神视频
0-1背包 完全背包_哔哩哔哩_bilibili
01背包(模板,可以配合该视频和代码随想录博客一起看)


恰好装这个容量,求方案数量的最大最小价值和,那就是把选最大值的操作换成加号
494. 目标和 - 力扣(LeetCode)
后续如果遇到其他两种变形笔者同步更新到这里
第一步:回溯法(深度优先遍历)
思路:
配合视频一起看更棒
0-1背包 完全背包_哔哩哔哩_bilibili
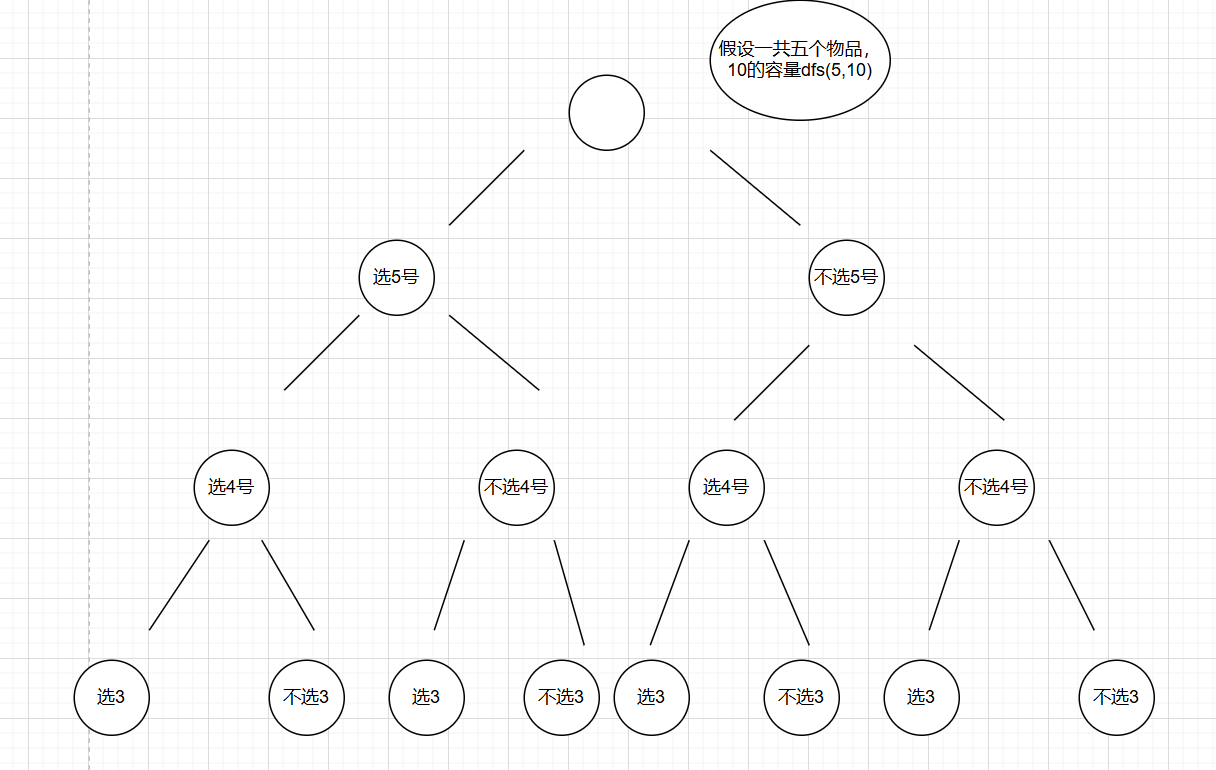
下面的就不画了,大家知道这个意思就行
选编号为i的话就是返回dfs(i-1,c-w[i])+v[i],就是代表已经把编号为i的物品已经放入了背包(表现为容量减了w[i],价值加了v[i]),然后继续递归下一个物品
不选编号为i的话就是返回dfs(i-1,c),这个代表的是一共有i-1个物品,总共是c的容量,那背包能装的最大价值是多少
我们本层函数会产生两个递归,一个是选了i,一个是没选i,返回的都是对应情况的最大值,我们要选最大的,所以要在这两个里面再选一个更大的作为返回值返回
从而得出了递推公式。
这个虽然过不了,时间复杂度太高,但是这是学习动态规划的必由之路
1.返回值和参数
w各个物品所占空间
v各个物品价值
i遍历物品
c是当前剩余的容量
返回值返回选或不选编号为i的物品的最大值
1
| int dfs(vector<int>& w,vector<int>& v,int i,int c)
|
2.终止条件
1
2
3
4
| if(i<0)
return 0;
if(c<w[i])
return dfs(w,v,i-1,c);
|
如果编号小于0说明已经到了树形结构最下面了,要开始从第一个物品选了,即自底(第一个物品)向上(i依次增大)开始遍历
如果当前容量已经小于要选的物品,那就直接返回给上层不选i号物品的结果
3.本层逻辑
在选和不选当前物品两种情况中(只要返回回来的一定是最大值),挑一个更大的返回
1
| return max(dfs(w,v,i-1,c),dfs(w,v,i-1,c-w[i])+v[i]);
|
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution {
public:
int dfs(vector<int>& w,vector<int>& v,int i,int c)
{
if(i<0)
return 0;
if(c<w[i])
return dfs(w,v,i-1,c);
return max(dfs(w,v,i-1,c),dfs(w,v,i-1,c-w[i])+v[i]);
}
int 01knapsack(vector<int>& nums,int c) {
vector<int> w(nums.begin(),nums.end());
vector<int> v(nums.begin(),nums.end());
return dfs(w,v,nums.size()-1,c);
}
};
|
C++还可用lambda来写
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public:
int 01knapsack(vector<int>& nums,int c) {
vector<int> w(nums.begin(),nums.end());
vector<int> v(nums.begin(),nums.end());
function<int(int,int)> dfs=[&](int i,int c)->int{
if(i<0)
return 0;
if(c<w[i])
return dfs(i-1,c);
return max(dfs(i-1,c),dfs(i-1,c-w[i])+v[i]);
};
return dfs(nums.size()-1,c);
}
};
|
第二步:改成记忆化搜索
注意,在递归函数中,我们同时有物品编号i和容量c,所以要用一个二维数组作为哈希表来存储计算结果进行复用。
然后在每次返回结果前都赋值一下,把计算结果给存储起来
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public:
int dfs(vector<int>& w,vector<int>& v,int i,int c,vector<vector<int>>& dp)
{
if(i<0)
return 0;
if(dp[i][c]!=-1)
return dp[i][c];
if(c<w[i])
return dp[i][c]=dfs(w,v,i-1,c,dp);
return dp[i][c]=max(dfs(w,v,i-1,c,dp),dfs(w,v,i-1,c-w[i],dp)+v[i]);
}
int 01knapsack(vector<int>& nums,int c) {
vector<int> w(nums.begin(),nums.end());
vector<int> v(nums.begin(),nums.end());
vector<vector<int>> dp(nums.size(),vector<int>(c+1,-1));
return dfs(w,v,nums.size()-1,c,dp);
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
int 01knapsack(vector<int>& nums,int c) {
vector<int> w(nums.begin(),nums.end());
vector<int> v(nums.begin(),nums.end());
vector<vector<int>> dp(nums.size(),vector<int>(c+1,-1));
function<int(int,int)> dfs=[&](int i,int c)->int{
if(i<0)
return 0;
if(dp[i][c]!=-1)
return dp[i][c];
if(c<w[i])
return dp[i][c]=dfs(i-1,c);
return dp[i][c]=max(dfs(i-1,c),dfs(i-1,c-w[i])+v[i]);
};
return dfs(nums.size()-1,c);
}
};
|
第三步:一比一翻译成动态规划(递推)
1.确定dp数组以及下标的含义
二维数组,dp[i][c]就是第i个物品在容量为c时可以取到的最大价值
i是物品编号
c是当前背包的总容量
2.确定递推公式
对应回溯算法本层逻辑部分
选或者不选第i号物品,如果没选,那就和上一个物品第i-1件遍历到j时一样的价值,因为没有选第i号
如果选了那就是 第i-1件物品在j-w[i]时的价值+选择的第i件物品的价值v[i]
1
| dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
|
3.dp数组如何初始化
全都初始化为0
第一行在容量大于第一件物品所需容量的时候就当做把第一件给放了进行初始化
因为dp[0][i]的物品编号只有0,即第一件物品,所以只能选择第一件物品得到最大价值,不选的话价值就为0
1
2
3
| vector<vector<int>> dp(nums.size(),vector<int>(c+1,0));
for(int i=w[0];i<=c;i++)
dp[0][i]=v[0];
|
4.确定遍历顺序
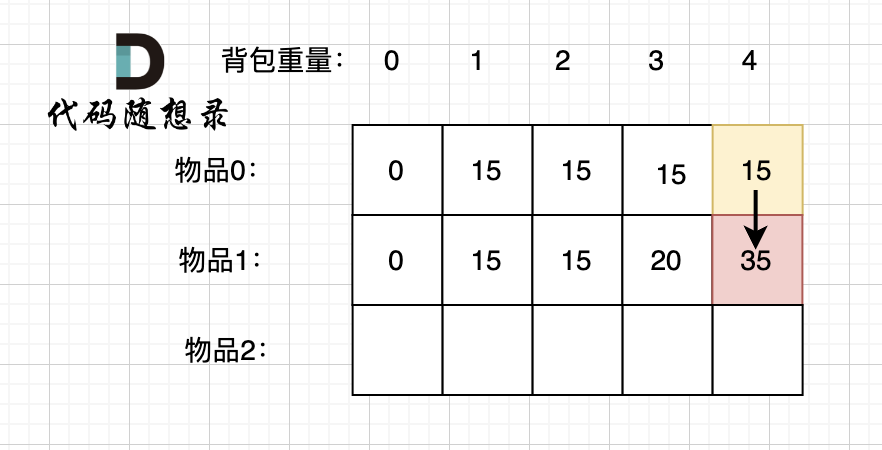
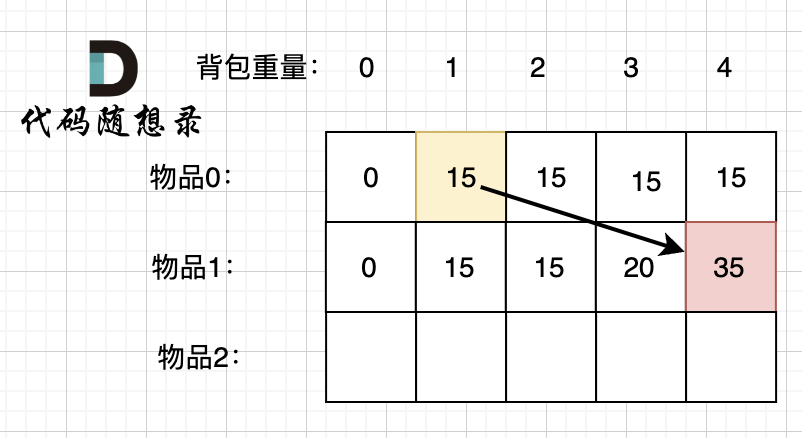
从前往后遍历,先遍历物品或者先遍历容量都是可以的,因为先物品是按照行一行一行来遍历,递推公式中的两个值都可以在遍历得出来,按照容量一列一列遍历也同样可以得出来这两个值
但仅限于二维,如果是一维那就只能先遍历物品后遍历容量,而且只能从后往前遍历容量
因为递推公式中用到的两个值在一维中变成了这样:
1
2
3
4
| vector<int> dp(c+1,0);
for(int i=0;i<nums.size();i++)
for(int j=c;j>=w[i];j--)
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
|
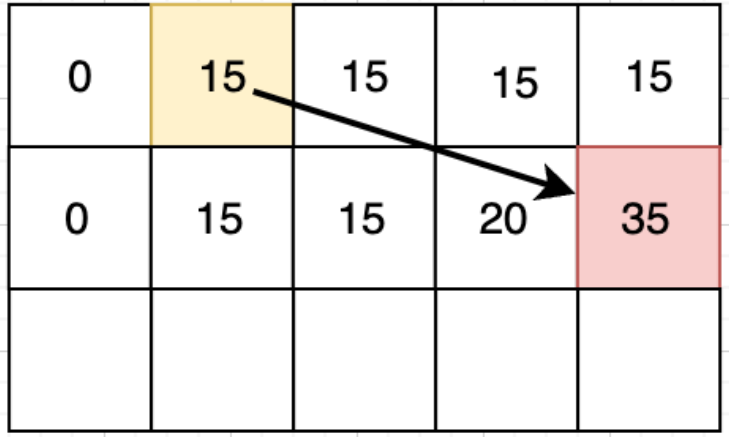
第一行是刷新前的数组,第二行是要对第一行进行覆盖的值,通过第一行的dp[j]和dp[j-w[i]]这两个值进行更新
如果从前往后,那dp[j-w[i]]就会被覆盖,从而得到一个错误的答案
如果不太理解可以转至:代码随想录
0-1背包 完全背包_哔哩哔哩_bilibili视频里面也会讲到滚动数组相关
1
2
3
4
5
6
| for(int i=1;i<nums.size();i++)
for(int j=0;j<=c;j++)
if(j>w[i])
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
else
dp[i][j]=dp[i-1][j];
|
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
int 01knapsack(vector<int>& nums,int c) {
vector<int> w(nums.begin(),nums.end());
vector<int> v(nums.begin(),nums.end());
vector<vector<int>> dp(nums.size(),vector<int>(c+1,0));
for(int i=w[0];i<=c;i++)
dp[0][i]=v[0];
for(int i=1;i<nums.size();i++)
for(int j=0;j<=c;j++)
if(j>w[i])
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
else
dp[i][j]=dp[i-1][j];
return dp[w.size()-1][c];
}
};
|
滚动数组代码
1
2
3
4
5
6
7
8
9
10
11
12
| class Solution {
public:
int 01knapsack(vector<int>& nums,int c) {
vector<int> w(nums.begin(),nums.end());
vector<int> v(nums.begin(),nums.end());
vector<int> dp(c+1,0);
for(int i=0;i<nums.size();i++)
for(int j=c;j>=w[i];j--)
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
return dp[c];
}
};
|

















