二叉树路径问题模板总结

问题分类

二叉树路径的问题大致可以分为两类：

1、自顶向下

一般是前序遍历

顾名思义，就是从某一个节点(不一定是根节点)，从上向下寻找路径，到某一个节点(不一定是叶节点)结束
具体题目如下：

257. 二叉树的所有路径 - 力扣（LeetCode）

112. 路径总和 - 力扣（LeetCode）

113. 路径总和 II - 力扣（LeetCode）

437. 路径总和 III - 力扣（LeetCode）

面试题 04.12. 求和路径 - 力扣（LeetCode）

988. 从叶结点开始的最小字符串 - 力扣（LeetCode）

而继续细分的话还可以分成一般路径与给定和的路径

自顶而下：
dfs，每次记得想想递归函数的本层逻辑，收集结果的条件，继续递归要传什么参数

//一般路径,即单纯收集路径：
	vector<vector<int>> res;
	void tra(TreeNode *t,vector<int> path)
    {
        if(t==nullptr)
            return;
        //递归函数的本层逻辑
        path.push_back(t->val);
        //收集结果
        if(t->left==nullptr&&t->right==nullptr)
                res.push_back(path);
        //继续递归
        tra(t->left,path);
        tra(t->right,path);
    }

//给定和的路径：
	vector<vector<int>> res;
    void tra(TreeNode *t,vector<int> path,int targetSum)
    {
        if(t==nullptr)
            return;
        //递归函数的本层逻辑
        targetSum-=t->val;
        path.push_back(t->val);
        //收集结果
        if(t->left==nullptr&&t->right==nullptr)
            if(targetSum==0)
                res.push_back(path);
        //继续递归
        tra(t->left,path,targetSum);
        tra(t->right,path,targetSum);
    }

这类题型DFS注意点：
1、如果是找路径和等于给定target的路径的，那么可以不用新增一个临时变量cursum来判断当前路径和，只需要用给定和target减去节点值，最终结束条件判断target==0即可

2、是否要回溯：二叉树的问题大部分是不需要回溯的，原因如下：
二叉树的递归部分(DFS)：tra(t->left),tra(t->right)已经把可能的路径穷尽了,
因此到任意叶节点的路径只可能有一条，绝对不可能出现另外的路径也到这个满足条件的叶节点的;

而对比二维数组(例如迷宫问题)的DFS,for循环向四个方向查找每次只能朝向一个方向，并没有穷尽路径，因此某一个满足条件的点可能是有多条路径到该点的

并且visited数组标记已经走过的路径是会受到另外路径是否访问的影响，这时候必须回溯

3、找到路径后是否要return:
取决于题目是否要求找到叶节点满足条件的路径,如果必须到叶节点,那么就要return;
但如果是到任意节点都可以，那么必不能return,因为这条路径下面还可能有更深的路径满足条件，还要在此基础上继续递归

4、是否要双重递归：看题目要不要求从根节点开始的，还是从任意节点开始（典型题目：437. 路径总和 III - 力扣（LeetCode））

257.二叉树的所有路径

257. 二叉树的所有路径 - 力扣（LeetCode）

这道题就是直接套用模板，只不过是vector path变成了string s，然后加上了->

这道题把递归函数的本层逻辑放到收集结果的前面是因为这样可以在加最后一个字符的时候不加->

class Solution {
public:
    vector<string> res;
    void tra(string s,TreeNode *t)
    {
        if(t==nullptr)
            return;
        if(t->left==nullptr&&t->right==nullptr)
        {
            s+=to_string(t->val);
            res.push_back(s);
            return;
        }
        s+=to_string(t->val);
        s+="->";
        tra(s,t->left);
        tra(s,t->right);
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        string s;
        tra(s,root);
        return res;
    }
};

112.路径总和

112. 路径总和 - 力扣（LeetCode）

class Solution {
public:
    bool flag=false;
    void tra(TreeNode *t,int target)
    {
        if(t==nullptr)
            return ;
        target-=t->val;
        if(t->left==nullptr&&t->right==nullptr)
        {
            if(target==0)
                flag=true;
        }
        tra(t->left,target);
        tra(t->right,target);
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        tra(root,targetSum);
        return flag;
    }
};

113.路径总和II

113. 路径总和 II - 力扣（LeetCode）

class Solution {
public:
    vector<vector<int>> res;
    void tra(TreeNode *t,vector<int> path,int targetSum)
    {
        if(t==nullptr)
            return;
        targetSum-=t->val;
        path.push_back(t->val);
        if(t->left==nullptr&&t->right==nullptr)
            if(targetSum==0)
                res.push_back(path);
        tra(t->left,path,targetSum);
        tra(t->right,path,targetSum);
    }
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        vector<int> path;
        tra(root,path,targetSum);
        return res;
    }
};

437.路径总和III

437. 路径总和 III - 力扣（LeetCode）

本题就不是从根节点到叶子节点，而是任意节点到任意节点，只要满足自顶向下即可

而我们之前用的模板其实是从根节点到叶子结点，接下来这么做

1.把判断是不是叶子节点的if去掉，那就是根节点到任意节点的路径

2.那么怎么从任意节点开始呢？

我们的backtracking是之前的从根节点到叶子节点的路径查询去掉了叶子结点的判断if，那就是根节点到任意路径，其实在这道题里面就是当传入的targetSum为0的时候，backtracking就会从传入的节点开始向下搜索，那我们再重新写一个遍历函数，把每个节点都当成根节点传一遍，那每个节点都会向下搜索路径，所以tra就是遍历这课树，遍历的时候让backtracking从当前结点开始向下搜索找到合适的路径

class Solution {
public:
    long long sum=0;
    void tra(TreeNode *t,long long targetSum)
    {
        if(t==nullptr)
            return;
        backtracking(t,targetSum);
        tra(t->left,targetSum);
        tra(t->right,targetSum);

    }
    void backtracking(TreeNode *t,long long targetSum)
    {
        if(t==nullptr)
            return;
        targetSum-=t->val;
        if(targetSum==0)
            sum++;
        backtracking(t->left,targetSum);
        backtracking(t->right,targetSum);
    }
    int pathSum(TreeNode* root, int targetSum) {
        tra(root,targetSum);
        return sum;
    }
};

注：这样做的复杂度较高，大家最好学习一下其他题解的时间复杂度较低的做法。

面试题 04.12.求和路径

面试题 04.12. 求和路径 - 力扣（LeetCode）

本题和路径总和III一样，不过多赘述

998.从叶节点开始的最小字符串

988. 从叶结点开始的最小字符串 - 力扣（LeetCode）

直接套用模板找出所有的路径最后sort排序即可

注意我们是从上面往下遍历的，要注意收集结果之前要把字符串反转一下

完整代码：

class Solution {
public:
    vector<string> res;
    void tra(TreeNode *t,string s)
    {
        if(t==nullptr)
            return ;
        s+='a'+t->val;
        if(t->left==nullptr&&t->right==nullptr)
        {
            reverse(s.begin(),s.end());
            res.push_back(s);
            return;
        }
        tra(t->left,s);
        tra(t->right,s);
    }
    string smallestFromLeaf(TreeNode* root) {
        string s;
        tra(root,s);
        sort(res.begin(),res.end());
        return res[0];
    }
};

2、非自顶向下

就是从任意节点到任意节点的路径，不需要自顶向下

一般是后序遍历

543. 二叉树的直径 - 力扣（LeetCode）

687. 最长同值路径 - 力扣（LeetCode）

124. 二叉树中的最大路径和 - 力扣（LeetCode）

二、非自顶而下：

这类题目一般解题思路如下：

设计一个后序遍历函数maxpath，调用自身求出以一个节点为根节点的左侧最长路径left和右侧最长路径right，那么经过该节点的最长路径就是left+right

接着只需要从根节点开始dfs,不断比较更新全局变量即可

int res=0;
int maxPath(TreeNode *root) //以root为路径起始点的最长路径
{
    if (!root)
        return 0;
    int left=maxPath(root->left);
    int right=maxPath(root->right);
    res = max(res, left + right + root->val); //更新全局变量  
    return max(left, right);   //返回左右路径较长者
}

这类题型DFS注意点：

1、left,right代表的含义要根据题目所求设置，比如最长路径、最大路径和等等

2、全局变量res的初值设置是0还是INT_MIN要看题目节点是否存在负值,如果存在就用INT_MIN，否则就是0

3、注意两点之间路径为1，因此一个点是不能构成路径的，但是如果是路径和的话就另说

4、res = max(res, left + right + root->val);

这个是关键，是以当前根结点为根结点的子树所能做出的最大路径，而在自底向上遍历的过程中，会把每

一个结点当做根节点看看当前子树的最大路径

5.return t->val+max(left, right);

这是第二个重点，这个保证了我们在树结构的每一层只会选择一个，要么左要么右，而不是既有左子树的

结点又有右子树的结点

543.二叉树的直径

543. 二叉树的直径 - 力扣（LeetCode）

1.函数参数以及返回值

maxDepth保存最大值

tra后序遍历进行路径选择

1 2	int maxDepth=-1; int tra(TreeNode *t)

2.终止条件

遇到空就返回0，因为这个对路径和或者最大路径长度的深度没有影响

1 2	if(t==nullptr) return 0;

3.本层递归函数逻辑

left记录左子树深度

right记录右子树深度

更新以当前结点为子树的深度（l+r+1）（包含当前结点的路径长度）和maxDepth之间的大小，最大值赋值给maxDepth

更新后，返回上层递归函数当前子树的最大深度

返回的子树最大深度是因为我们在父节点进行路径选择的时候，当前结点的左右子树不可以同时被选

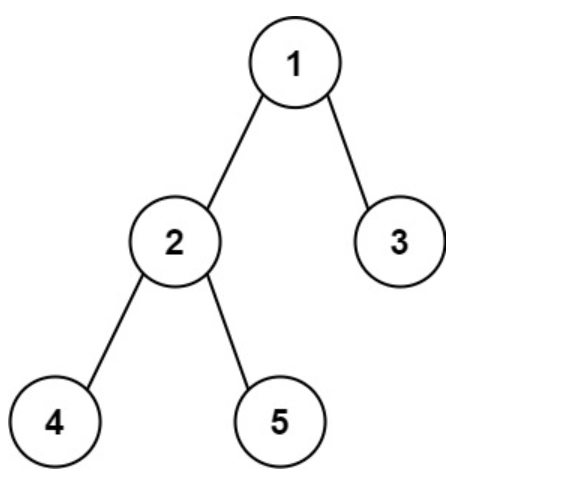
举个例子 2为当前结点，那我们往1这个父节点返回的时候，4,2和5,2这两条路径只能选择一条，我们挑最大的给父节点

而不是4,2,5这种路径返回给父节点，因为1,2,4,5这种路径是非法的

我们只能是1,2,4或者1,2,5这种的路径

int left=tra(t->left);
int right=tra(t->right);
maxDepth=max(maxDepth,left+right+1);
return 1+max(left,right);

完整代码：

class Solution {
public:
    int maxDepth=-1;
    int tra(TreeNode *t)
    {
        if(t==nullptr)
            return 0;
        int left=tra(t->left);
        int right=tra(t->right);
        maxDepth=max(maxDepth,left+right+1);
        return 1+max(left,right);
    }
    int diameterOfBinaryTree(TreeNode* root) {
        if(root==nullptr)
            return 0;
        int t=tra(root);
        return maxDepth-1;
    }
};

124.二叉树中的最大路径和

124. 二叉树中的最大路径和 - 力扣（LeetCode）

1.函数参数以及返回值

maxSum保存最大值

choosePath后序遍历进行路径选择

1 2	int maxSum=INT_MIN; int choosePath(TreeNode *t)

2.终止条件

遇到空就返回0，因为这个对路径和或者最大路径长度的深度没有影响

1 2	if(t==nullptr) return 0;

3.本层递归函数逻辑

1.后序遍历

2.maxSum更新操作表示以当前结点为根结点的子树的最大路径长度或者最大路径和

3.在l和r的地方也要注意，因为题目有负值，所以返回值要和0作比较，如果返回值是个负数，那说明l选择的路径的结点我们都不选，因为对最大路径和是负作用。

4.最后返回值地方返回max(l,r)选择左子树或者右子树其中一个，这样避免了选择同时有左子树和右子树的情况

int l=max(choosePath(t->left),0);
int r=max(choosePath(t->right),0);
maxSum=max(maxSum,l+r+t->val);
return t->val+max(l,r);

完整代码：

class Solution {
public:
    int maxSum=INT_MIN;
    int choosePath(TreeNode *t)
    {
        if(t==nullptr)
            return 0;
        int l=max(choosePath(t->left),0);
        int r=max(choosePath(t->right),0);
        maxSum=max(maxSum,l+r+t->val);
        return t->val+max(l,r);
    }
    int maxPathSum(TreeNode* root) {
        int res=choosePath(root);
        return maxSum;
    }
};

687.最长同值路径

687. 最长同值路径 - 力扣（LeetCode）

1.函数参数以及返回值

maxDepth保存最大值

tra后序遍历进行路径选择

1 2	int res=0; int tra(TreeNode *t)

2.终止条件

遇到空就返回0，因为这个对路径和或者最大路径长度的深度没有影响

1 2	if(t==nullptr) return 0;

3.本层递归函数逻辑

left记录左子树相同

right记录右子树深度

1.后序遍历

2.res更新操作表示以当前结点为根结点的子树的最大路径长度或者最大路径和。大家可能对这里有疑惑，觉得你怎么知道当前结点和左右子树全都是一样的值呢？如果不知道的话怎么可以写r+l呢？

其实是这样的，如果上面的判断，左边和当前的节点一样，那当前节点和左子树就可以连上，如果不一样那就直接把l=0，就相当于把左子树给砍掉了。同理，如果右子树也一样。

而如果可以连上，那说明l+r就是对的，就是以当前结点为根结点的子树中的最长同值路径。

3.在l和r的地方也要注意，因为题目是判断是否相同，所以要进行判断，左右子树返回值分别和当前节点的值进行比较，相等的话就在下层子树返回的基础上++，一旦不相同就要置为0，因为要求连续相等路径，而这条路径相当于已经断了。不用担心前面的没有保存上，res更新的时候会把它给记录下来。

4.最后返回值地方返回max(l,r)选择左子树或者右子树其中一个，这样避免了选择同时有左子树和右子树的情况

int l=tra(t->left);
int r=tra(t->right);
if(t->left&&t->val==t->left->val)
	l++;
else
	l=0;
if(t->right&&t->right->val==t->val)
	r++;
else
	r=0;
res=max(res,r+l);
return max(l,r);

完整代码：

class Solution {
public:
    int res=0;
    int tra(TreeNode *t)
    {
        if(t==nullptr)
            return 0;
        int l=tra(t->left);
        int r=tra(t->right);
        if(t->left&&t->val==t->left->val)
            l++;
        else
            l=0;
        if(t->right&&t->right->val==t->val)
            r++;
        else
            r=0;
        res=max(res,r+l);
        return max(l,r);
    }
    int longestUnivaluePath(TreeNode* root) {
        int r=tra(root);
        return res;
    }
};