26考研 | 王道 | 数据结构 | 第四章串

第四章串

0.本节全部代码

#include<iostream>

using namespace std;

const int MAXSIZE = 255;

/*
假设有串 T = '', S = 'iPhone 11 Pro Max?', W = 'Pro'

1. StrAssign(&T, chars)： 赋值操作，把串T赋值为chars。
2. StrCopy(&T, S) :：复制操作，把串S复制得到串T。
3. StrEmpty(S)：判空操作，若S为空串，则返回TRUE，否则返回False。
4. StrLength(S)：求串长，返回串S的元素个数。
5. ClearString(&S)：清空操作，将S清为空串。
6. DestroyString(&S)：销毁串，将串S销毁（回收存储空间）。
7. Concat(&T, S1, S2)：串联接，用T返回由S1和S2联接而成的新串。
8. SubString(&Sub, S, pos, len)求子串，用Sub返回串S的第pos个字符起长度为len的子串.
9. Index(S, T)：定位操作，若主串S中存在与串T值相同的子串，则返回它再主串S中第一次出现的位置，否则函数值为0.
10. StrCompare(S, T)：串的比较操作，参照英文词典排序方式；若S > T, 返回值 > 0; S = T, 返回值 = 0 (需要两个串完全相同); S < T, 返回值 < 0.
*/

struct _string {
	char data[MAXSIZE];
	int length;
};

//打印串的内容
void printfstring(_string t)
{
	for (int i = 1; i <= t.length; i++)
		cout << t.data[i];
	cout << endl;
}

//赋值操作，把串T赋值为chars
bool StrAssign(_string &t, char *s)
{
	t.length = 0;
	for (int i = 1; s[i]!='\0'; i++)
	{
		t.data[i] = s[i];
		t.length++;
	}
	return true;
}

//复制操作，把串S复制得到串T
bool StrCopy(_string& t,_string s)
{
	if (s.length > MAXSIZE)
		return false;
	t.length = s.length;
	for (int i = 1; i <= s.length; i++)
	{
		t.data[i] = s.data[i];
	}
	return true;
}

//：判空操作，若S为空串，则返回TRUE，否则返回False
bool StrEmpty(_string s)
{
	return s.length == 0;
}

//求串长，返回串S的元素个数
int StrLength(_string s)
{
	return s.length;
}

//清空操作，将S清为空串
void ClearString(_string &s)
{
	s.length = 0;
}

//销毁串，将串S销毁（回收存储空间）----系统自动回收不需要管
void DestroyString(_string& s)
{

}

//串联接，用T返回由S1和S2联接而成的新串
bool Concat(_string&t,_string s1,_string s2)
{
	if (s1.length + s2.length > MAXSIZE)
		return false;
	t.length = s1.length + s2.length;
	for (int i = 1; i <= s1.length; i++)
		t.data[i] = s1.data[i];
	for (int i = s1.length + 1; i <= s1.length + s2.length; i++)
		t.data[i] = s2.data[i - s1.length];
	return true;
}

//求子串，用Sub返回串S的第pos个字符起长度为len的子串.
bool SubString(_string &sub,_string s,int pos,int len)
{
	if (pos + len - 1 > s.length)
		return false;
	sub.length = len;
	for (int i = pos, j = 1; i <= pos + len; i++, j++)
		sub.data[j] = s.data[i];
	return true;
}

//串的比较操作，参照英文词典排序方式；若S > T, 返回值 > 0; S = T, 返回值 = 0 (需要两个串完全相同); S < T, 返回值 < 0.
bool StrCompare(_string s,_string t)
{
	for (int i = 1; i <= s.length && i <= t.length; i++)
		if (s.data[i] != t.data[i])
			return s.data[i] > t.data[i];
	return s.length > t.length;
}

//朴素匹配 ：定位操作，若主串S中存在与串T值相同的子串，则返回它再主串S中第一次出现的位置，否则函数值为0.
int Index(_string s,_string t)
{
	for (int i = 1; i <= s.length - t.length + 1; i++)
	{
		int j = 1;
		for (j = 1; j <= t.length; j++)
			if (s.data[i + j - 1] != t.data[j])
				break;
		if (j == t.length + 1)
			return i;
	}
	return 0;
}

// 获取模式串T的next[]数组
void getNext(_string T, int next[]) {
	int i = 1, j = 0;
	next[1] = 0;
	while (i < T.length) {
		if (j == 0 || T.data[i] == T.data[j]) {
			++i; 
			++j;
			next[i] = j;
		}
		else
			j = next[j];
	}
}

// KPM算法，求主串S中模式串T的位序，没有则返回0
int Index_KPM(_string S, _string T) {
	int i = 1, j = 1;
	int next[MAXSIZE];//int next[T.length + 1];
	getNext(T, next);
	while (i <= S.length && j <= T.length) {
		if (j == 0 || S.data[i] == T.data[j]) {
			++i; ++j;
		}
		else
			j = next[j];
	}
	if (j > T.length)
		return i - T.length;
	else
		return 0;
}


int main()
{
	
	char ch[17] = "0helloaaaaaaaaab";
	_string s;
	StrAssign(s, ch);
	cout << StrEmpty(s) << endl;
	printfstring(s);
	cout << StrLength(s) << endl;
	_string t;
	char ch2[17] = "0";
	StrAssign(t, ch2);
	StrCopy(t,s);
	cout << StrLength(t) << endl;
	cout << StrEmpty(t) << endl;
	printfstring(t);
	//ClearString(t);
	cout << StrEmpty(t) << endl;
	cout << StrLength(t) << endl;

	_string a;
	StrAssign(a, ch2);
	Concat(a, s, t);
	printfstring(a);
	cout << StrLength(a) << endl;
	_string b;
	StrAssign(b, ch2);
	SubString(b, a, 5, 5);
	printfstring(b);
	cout << StrCompare(a, b) << endl;

	cout << Index(a, b) << endl;
	cout << Index(a, s) << endl;
	_string c;
	StrAssign(c, ch2);
	SubString(c, s, 11, 5);
	printfstring(c);
	cout << Index(s, c) << endl;
	
	//KMP测试
	char ch3[8] = "0ababaa";
	_string ss;
	StrAssign(ss, ch3);
	int next[9] = { 0 };
	getNext(ss, next);
	for (int i = 1; i <= 6; i++)
		cout << next[i] << " ";
	cout << endl;

	cout << Index_KPM(a, b) << endl;
	cout << Index_KPM(a, s) << endl;
	return 0;
}

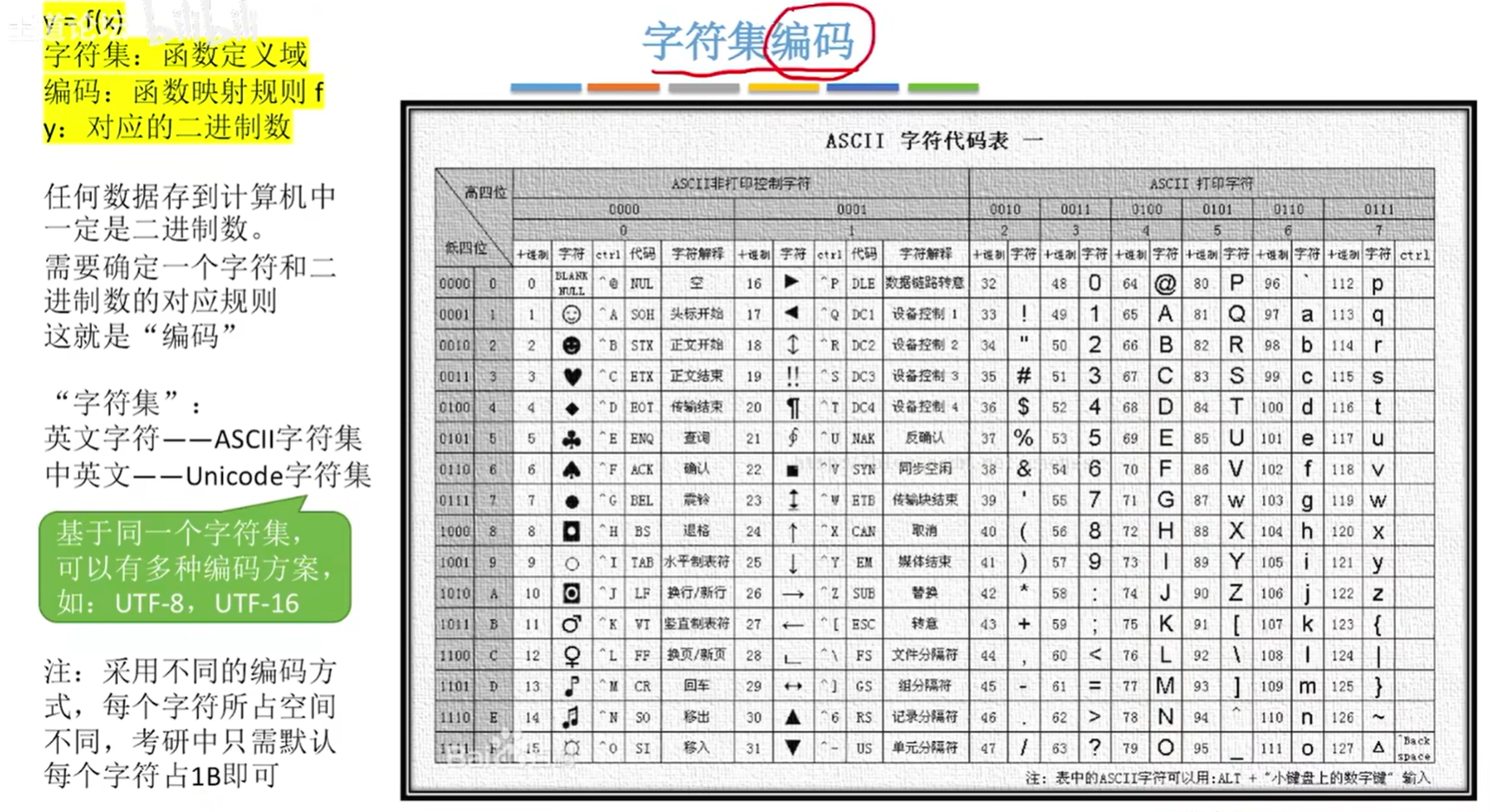
4.1. 串的基本概念

串，即字符串 (String) 是由零个或多个字符组成的有限序列。一般记为S=’a1a2…..·an’(n>=0)
其中，S是串名，单引号括起来的字符序列是串的值;a;可以是字母、数字或其他字符;串中字符的个数n称为串的长度。n =0时的串称为空串。

例:

1 2	S="HelloWorld!" T='iPhone 11 Pro Max?'

子串:串中任意个连续的字符组成的子序列。
主串:包含子串的串。
字符在主串中的位置:字符在串中的序号。
子串在主串中的位置:子串的第一个字符在主串中的位置。（位序是从1开始而不是0）
串是一种特殊的线性表，数据元素之间呈线性关系，但是对线性表的元素类型做出了要求，只可以是字符集之中的内容
串的数据对象限定为字符集（如中文字符、英文字符、数字字符、标点字符等）
串的基本操作，如增删改查等通常以子串为操作对象。

4.2. 串的基本操作

假设有串 T = ‘’, S = ‘iPhone 11 Pro Max?’, W = ‘Pro’

StrAssign(&T, chars)：赋值操作，把串T赋值为chars。
StrCopy(&T, S):：复制操作，把串S复制得到串T。
StrEmpty(S)：判空操作，若S为空串，则返回TRUE，否则返回False。
StrLength(S)：求串长，返回串S的元素个数。
ClearString(&S)：清空操作，将S清为空串。
DestroyString(&S)：销毁串，将串S销毁（回收存储空间）。
Concat(&T, S1, S2)：串联接，用T返回由S1和S2联接而成的新串。
SubString(&Sub, S, pos, len)求子串，用Sub返回串S的第pos个字符起长度为len的子串.
Index(S, T)：定位操作，若主串S中存在与串T值相同的子串，则返回它再主串S中第一次出现的位置，否则函数值为0.
StrCompare(S, T)：串的比较操作，参照英文词典排序方式；若S > T,返回值>0; S = T,返回值=0 (需要两个串完全相同) ; S < T,返回值<0.

4.3. 串的存储实现

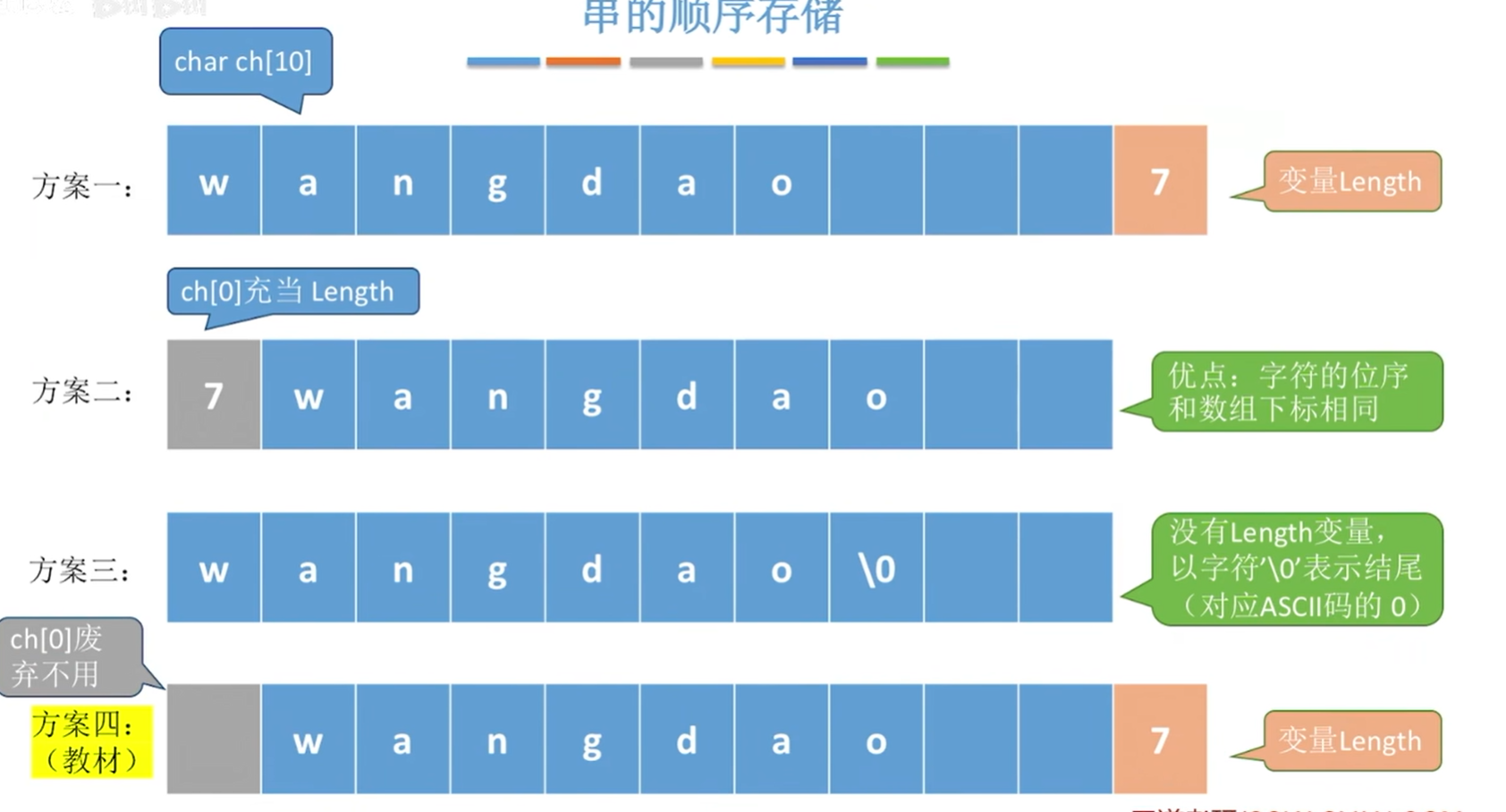
顺序存储的三个方案：

1.专门用新的变量length存储长度

2.直接在数组第一个位置存储长度

优：下标和位序一一对应，不需要转换

缺：其实第一个位置也就是一字节，一字节就是8bit，最大也就是255，这个会限制字符串的长度

3.不设置length，以\0作为字符串的结束标志

这个很麻烦，要想知道长度必须遍历一遍

4.废弃第一个位置不用，同时也设置length记录数组长度

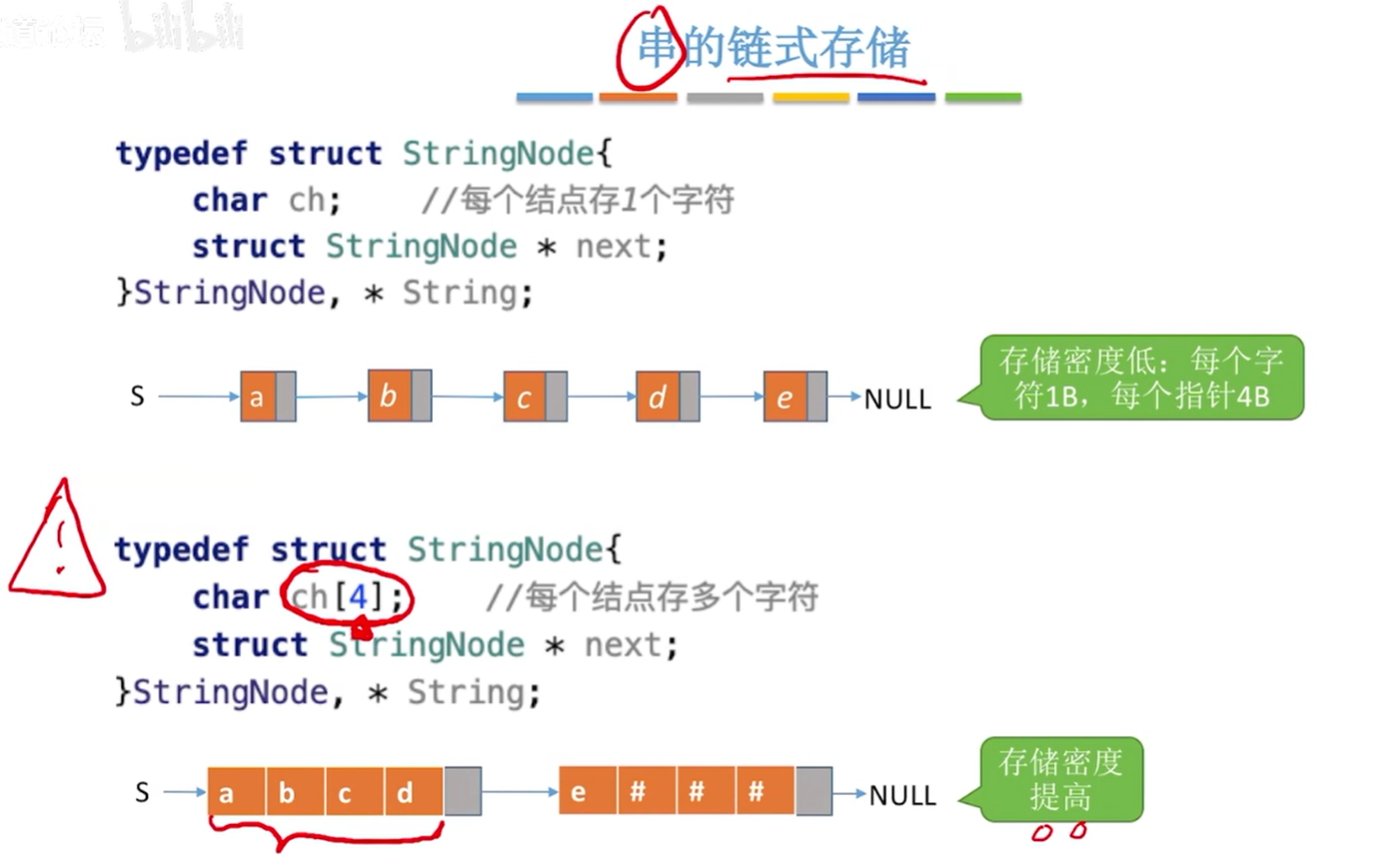
4.3.1 静态数组实现

静态数组实现(定长顺序存储)

#define MAXLEN 255   //预定义最大串长为255
 
typedef struct{
    char ch[MAXLEN];   //静态数组实现（定长顺序存储）
                       //每个分量存储一个字符
                       //每个char字符占1B
    int length;        //串的实际长度
}SString;

动态数组实现( 堆分配存储)

typedef struct{
    char *ch;          //按串长分配存储区，ch指向串的基地址
    int length;        //串的实际长度
}HString;
HString S;
S.ch = (char*)malloc(MAXLEN *sizeof(char));
S.length = 0;

4.3.2 基本操作的实现

#define MAXLEN 255
 
typedef struct{
    char ch[MAXLEN];   
    int length;       
}SString;
 
// 1. 求子串
bool SubString(SString &Sub, SString S, int pos, int len){
    //子串范围越界
    if (pos+len-1 > S.length)
        return false;
    
    for (int i=pos; i<pos+len; i++)
        Sub.cn[i-pos+1] = S.ch[i];
    
    Sub.length = len;
 
    return true;
}
 
// 2. 比较两个串的大小
int StrCompare(SString S, SString T){
    for (int i; i<S.length && i<T.length; i++){
        if(S.ch[i] != T.ch[i])
            return S.ch[i] - T.ch[i];
    }
    //扫描过的所有字符都相同，则长度长的串更大
    return S.length - T.length;
}
 
// 3. 定位操作
int Index(SString S, SString T){
    int i=1;
    n = StrLength(S);
    m = StrLength(T);
    SString sub;        //用于暂存子串
 
    while(i<=n-m+1){
        SubString(Sub,S,i,m);
        if(StrCompare(Sub,T)!=0)
            ++i;
        else 
            return i;    // 返回子串在主串中的位置
    }
    return 0;            //S中不存在与T相等的子串
}

4.4. 串的朴素模式匹配

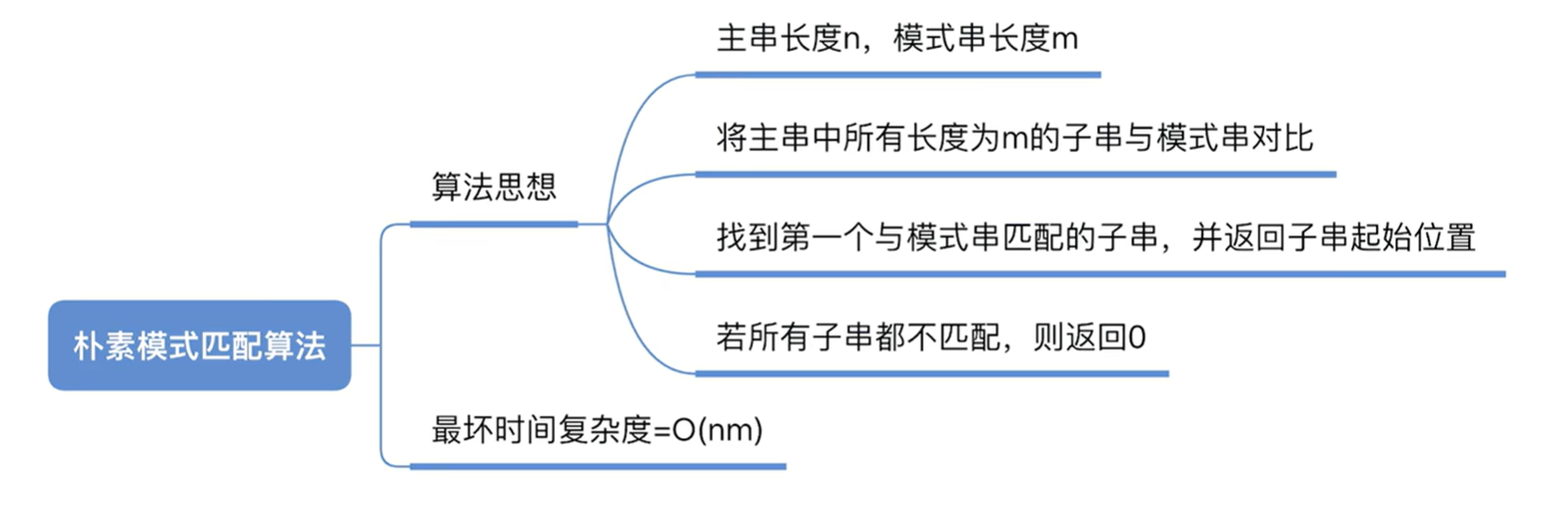
就是个暴力解法

串的模式匹配：在主串中找到与模式串相同的子串，并返回其所在主串中的位置。

朴素模式匹配算法(简单模式匹配算法) 思想:

将主串中与模式串长度相同的子串搞出来，挨个与模式串对比当子串与模式串某个对应字符不匹配时，就立即放弃当前子串，转而检索下一个子串。
若模式串长度为m，主串长度为n，则直到匹配成功/匹配失败最多需要(n-m+1)*m 次比较最坏时间复杂度: 0(nm)
最坏情况:每个子串的前m-1个字符都和模式串匹配，只有第m个字符不匹配。
比较好的情况:每个子串的第1个字符就与模式串不匹配

串的朴素模式匹配算法代码实现：

// 在主串S中找到与模式串T相同的子串并返回其位序，否则返回0
int Index(SString S, SString T){   
    int k=1;    
    int i=k, j=1;  
    while(i<=S.length && j<=T.length){    
        if(S.ch[i] == T.ch[j]){     
            ++i; ++j; 
        }else{        
            k++; i=k; j=1; 
        }   
    }   
    if(j>T.length) 
        return k;   
    else       
        return 0;
}

或者不用k的方式：

int Index(SString S, SString T){
    int i=1;                //扫描主串S
    int j=1;                //扫描模式串T
    while(i<=S.length && j<=T.length){
        if(S.ch[i] == T.ch[j]){
            ++i;
            ++j;             //继续比较后继字符
        }
        else{
            i = i-j+2;
            j=1;             //指针后退重新开始匹配
        }
    }
    if(j>T.length)
        return i-T.length;
    else
        return 0;
}

时间复杂度：设模式串长度为m，主串长度为n

匹配成功的最好时间复杂度：O(m)
匹配失败的最好时间复杂度：O(n)
最坏时间复杂度：O(nm)

4.5. KPM算法

算法思想

朴素模式匹配算法的缺点:当某些子串与模式串能部分匹配时，主串的扫描指针 i 经常回溯，导致时间开销增加。最坏时间复杂度O(nm)。
KMP算法:当子串和模式串不匹配时，主串指针i不回溯，模式串指针j = next[ j ]算法平均时间复杂度：O(n+m)。

求模式串的next数组

串的前缀:包含第一个字符，且不包含最后一个字符的子串。
串的后缀:包含最后一个字符，且不包含第一个字符的子串。
当第i个字符匹配失败，由前 1~j-1 个字符组成的串记s，next[i]为s的最长相等前后缀长度+1特别地，next[1]=0
算出最长相等前后缀长度+1是因为我们的字符串下标是从1开始的，如果是从0开始的，那就不可以初始化为0而是-1了，因为s[0]是有元素的，下面的ababaa的next数组就不是0,1,1,2,3,4而是-1,0,0,1,2,3了
而next数组下标从1开始也是为了和字符串下标为1开始对齐，好表示一些，正常而言next从0开始，那么求出来的next[i-1]才是第i个元素不匹配的时候的要回溯到的地方，而如果从1开始，那么next[i]就是第i个元素不匹配的时候的要回溯到的地方

以ababaa作为举例吧

初始化next[1]=0;

当i=2匹配失败的时候，看前i-1个字母组成的s即 a，由于a既是首字母又是尾字母，那最长相等前后缀就是0，再加1就是1

当i=3匹配失败的时候，看前i-1个字母组成的s即 ab，那最长相等前后缀就是0，再加1就是1

当i=4匹配失败的时候，看前i-1个字母组成的s即 aba，那最长相等前后缀a，就是1，再加1就是2

当i=5匹配失败的时候，看前i-1个字母组成的s即 abab，那最长相等前后缀ab，就是2，再加1就是3

当i=6匹配失败的时候，看前i-1个字母组成的s即 ababa，那最长相等前后缀aba，就是3，再加1就是4

即为 0,1,1,2,3,4

再说一下nextval怎么求

1.先求出next数组

2.逐个分析，如果第i个字母和nextval[i]这个下标所对应的字母相同，那么nextval[i]=nextval[nextval[i]]

举例：

令s字符串为ababaa
a ,b ,a ,b ,a ,a的next数组为
0 ,1 ,1 ,2 ,3 ,4

i=1,nextval[1]=0
从i=2开始
s[2]=b不等于s[next[2]]=s[1]所对应的字母a，所以nextval[2]还等于1
i=3
s[3]=a等于s[next[3]]=s[1]所对应的字母a，所以nextval[3]等于next[1]=0
i=4
s[4]=b等于s[next[4]]=s[2]所对应的字母b，所以nextval[4]等于next[1]=1
i=5
s[5]=a等于s[next[5]]=s[3]所对应的字母a，所以nextval[5]等于next[1]=0(注意此时nextval[1]就已经是0了)
i=6
s[6]=a不等于s[next[6]]=s[4]所对应的字母b，所以nextval[6]等于next[6]=4(注意此时nextval[1]就已经是0了)

所以最后就是0,1,0,1,0，4

KPM 算法代码实现：

// 获取模式串T的next[]数组
void getNext(SString T, int next[]){ 
    int i=1, j=0;  
    next[1]=0;  
    while(i<T.length){   
        if(j==0 || T.ch[i]==T.ch[j]){ 
            ++i; ++j;      
            next[i]=j;  
        }else      
            j=next[j]; 
    }
}
 
// KPM算法，求主串S中模式串T的位序，没有则返回0
int Index_KPM(SString S, SString T){   
    int i=1, j=1;  
    int next[T.length+1]; 
    getNext(T, next);  
    while(i<=S.length && j<=T.length){  
        if(j==0 || S.ch[i]==T.ch[j]){   
            ++i; ++j;   
        }else   
            j=next[j];   
    }    
    if(j>T.length)   
        return i-T.length;  
    else
        return 0;
}
 
int main() {
	SString S={"ababcabcd", 9};
	SString T={"bcd", 3};
	printf("%d ", Index_KPM(S, T));	//输出9
}

KPM 算法的进一步优化：

改进 next 数组：

void getNextval(SString T, int nextval[]){
    int i=1,j=0;
    nextval[1]=0;
    while(i<T.length){
        if(j==0 || T.ch[i]==T.ch[j]){
            ++i; ++j;
            if(T.ch[i]!=T.ch[j])
                nextval[i]=j;
            else
                nextval[i]=nextval[j];
        }else
            j=nextval[j];
    }
}