Day91 | 灵神 | 二叉树二叉树的最小深度

111.二叉树的最小深度

`后序遍历思路：`

1.递归函数意义

求得以传入参数t为根节点的树的最小深度

2.参数和返回值

1	int get_depth(TreeNode *t)

返回值就是以t为根结点的树的最小深度

3.终止条件（边界条件）

如果我们碰到了空节点，那么它的深度肯定就是0了

1 2	if(t==nullptr) return 0;

4.本层逻辑（非边界条件）

如果 node 是空节点，由于没有节点，返回 0。

如果 node 没有右儿子，那么深度就是左子树的深度加一，即 dfs(node)=dfs(node.left)+1。

如果 node 没有左儿子，那么深度就是右子树的深度加一，即 dfs(node)=dfs(node.right)+1。

如果 node 左右儿子都有，那么分别递归计算左子树的深度，以及右子树的深度，二者取最小值再加一，即
dfs(node)=min(dfs(node.left),dfs(node.right))+1

if(t->left==nullptr)
    return get_depth(t->right)+1;
if(t->right==nullptr)  
    return get_depth(t->left)+1;
return min(get_depth(t->left),get_depth(t->right))+1;

5.和最大深度的区别

为什么相比最大深度多了两个if？

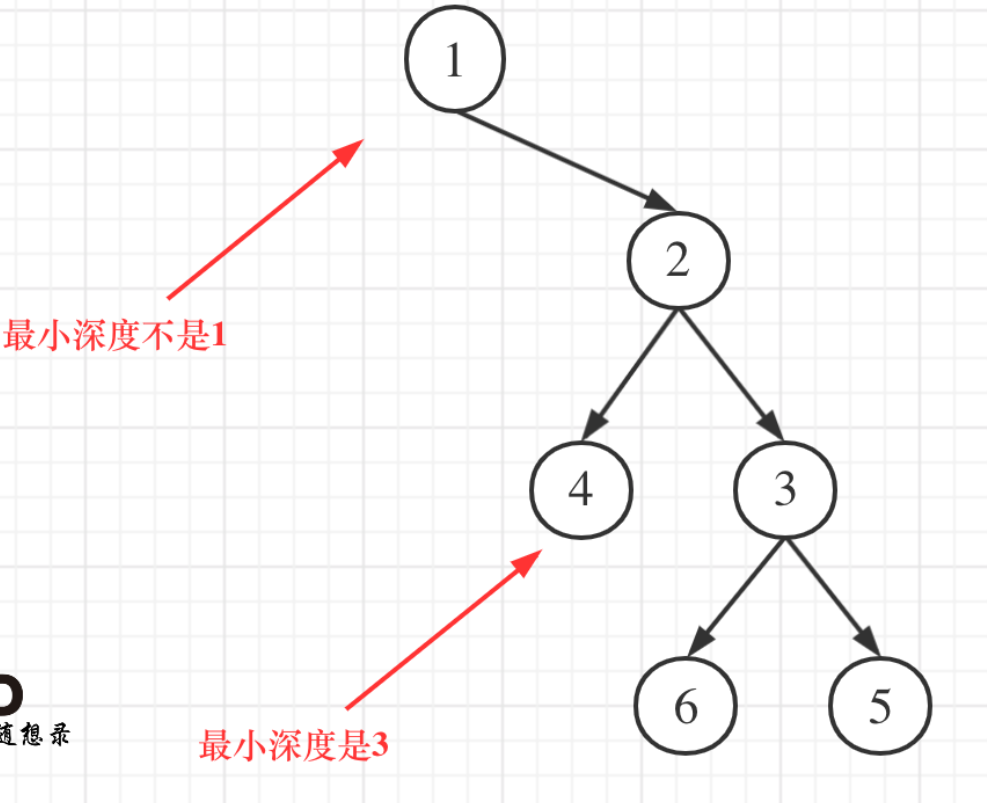
这个左子树为空，所以如果按照上一题的写法，最小深度就直接是1了，因为取的是左右子树的最小值

而实际上我们应该返回的是，右子树的最小深度+1

右子树为空时同理

把上图右子树看做一个整体，这其实也可以看做是数学归纳法里面的n等于1的边界条件的情况(个人认为)

完整代码：

class Solution {
public:
    int get_depth(TreeNode *t)
    {
        if(t==nullptr)
            return 0;
        if(t->left==nullptr)
            return get_depth(t->right)+1;
        if(t->right==nullptr)  
            return get_depth(t->left)+1;
        return min(get_depth(t->left),get_depth(t->right))+1;
    }
    int minDepth(TreeNode* root) {
        return get_depth(root);        
    }   
};

`方法二：深度优先搜索`

思路及解法

首先可以想到使用深度优先搜索的方法，遍历整棵树，记录最小深度。

对于每一个非叶子节点，我们只需要分别计算其左右子树的最小叶子节点深度。这样就将一个大问题转化为了小问题，可以递归地解决该问题。

class Solution {
public:
    int minDepth(TreeNode *root) {
        if (root == nullptr) {
            return 0;
        }
	if (root->left == nullptr && root->right == nullptr) {
        return 1;
    }

    int min_depth = INT_MAX;
    if (root->left != nullptr) {
        min_depth = min(minDepth(root->left), min_depth);
    }
    if (root->right != nullptr) {
        min_depth = min(minDepth(root->right), min_depth);
    }

    return min_depth + 1;
}
};

复杂度分析

时间复杂度：O(N)，其中 N 是树的节点数。对每个节点访问一次。

空间复杂度：O(H)，其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 O(logN)。

`方法三：广度优先搜索`

思路及解法

同样，我们可以想到使用广度优先搜索的方法，遍历整棵树。

当我们找到一个叶子节点时，直接返回这个叶子节点的深度。广度优先搜索的性质保证了最先搜索到的叶子节点的深度一定最小。

class Solution {
public:
    int minDepth(TreeNode *root) {
        if (root == nullptr) {
            return 0;
        }
	queue<pair<TreeNode *, int> > que;
    que.emplace(root, 1);
    while (!que.empty()) 
    {
        TreeNode *node = que.front().first;
        int depth = que.front().second;
        que.pop();
        if (node->left == nullptr && node->right == nullptr) {
            return depth;
        }
        if (node->left != nullptr) {
            que.emplace(node->left, depth + 1);
        }
        if (node->right != nullptr) {
            que.emplace(node->right, depth + 1);
        }
    }

    return 0;
}
};