Day106 | 灵神 | 二叉树 二叉树中的最长交错路径
Day106 | 灵神 | 二叉树 二叉树中的最长交错路径
1372.二叉树中的最长交错路径
1372. 二叉树中的最长交错路径 - 力扣(LeetCode)
笔者题解
思路:
这道题挺难想的,笔者第一次写,没写出来,原因是情况少了,只考虑可以往左的时候往左和可以往右走的时候往右,少了不可以往左的时候往左和不可以往右的时候往右走
所以就是分四种情况,同时我们使用一个bool值flag记录上一次我们是从左边来的还是从右边来的,同时使用len记录路径长度,dfs含义就是深度搜索,但是要在搜索过程中记录最大值
规定flag为0,表示可以往左走,不可以往右走,表示我们上次走的右子树到达了本节点
flag为1,表示可以往右走,不可以往左走,表示我们上次走的左子树到达了本节点
1 | void dfs(TreeNode *t,bool flag,int len) |
1.可以往左的时候往左
1 | if(!flag) |
flag为0,这说明我们可以往左走,然后下一层的递归函数就不可以往左走只可以往右走,所以传入1,并且长度为原来长度加上本层节点就是len+1
2.可以往右走的时候往右
1 | if(flag) |
flag为1,那说明我们可以往右走,然后下一层的递归函数就不可以往右走只能往左走,所以传入0,并且长度为原来长度加上本层节点就是len+1
3.不可以往右的时候往右走
1 | if(!flag) |
flag为0,这说明我们可以往左走。但是我们没选择往左走,而是往右走了,可是这样就不符合题意了。那没办法了只能把前面积累的长度都清空然后从当前结点重新算了
所以我们这次选择往右走,所以下一层递归函数不可以往右,传入0,长度从当前节点重新计算,所以传入1
4.不可以往左的时候往左
1 | if(flag) |
flag为1,这说明我们可以往右走。但是我们没选择往右走,而是往左走了,可是这样就不符合题意了。那没办法了只能把前面积累的长度都清空然后从当前结点重新算了
所以我们这次选择往左走,所以下一层递归函数不可以往左,传入1,长度从当前节点重新计算,所以传入1
完整代码:
1 | class Solution { |
大佬解法
这是笔者自己的理解
用l和r记录长度,l就是上层结点走左子树来到本节点的长度,r就是上层结点走右子树来到本节点的长度
如果我们在本层结点想走左子树,那么下一层的l就是r+1,r就是0
l=r+1的原因是,我们上一次走的右子树那么在本层节点才可以走左子树
r=0的原因是,我们是走的左子树,所以从右子树去的路径长度就归0了
同理,如果我们本层结点想走右子树,下一层的l就是0,r就是l+1
这个可行在于,一个节点没办法被父节点既选择向左又选择向右,要么跟随父节点向左,那就+1,要么自己向右,那就从0开始,反之亦然
1 | class Solution { |
大佬自己的题解
思路
采用深度优先遍历的方式,我们可以从顶向下访问到所有节点。并且遍历下一个子节点时,我们也能够知道子节点是属于父节点的左子树,还是右子树。
所以我们可以为每个节点缓存两个值,一个l表示到达当前节点时,该节点为左子树时的路径数,一个r表示该节点为右子树时的到达路径。
当然,一个节点要么是左子树,要么是右子树,所以l和r其中只有一个有值。
那么在遍历该节点的子节点时,如果子节点是左子树,那么它的l值就是父节点的r值加1. 如果是右子树,就是父节点的l值加1.
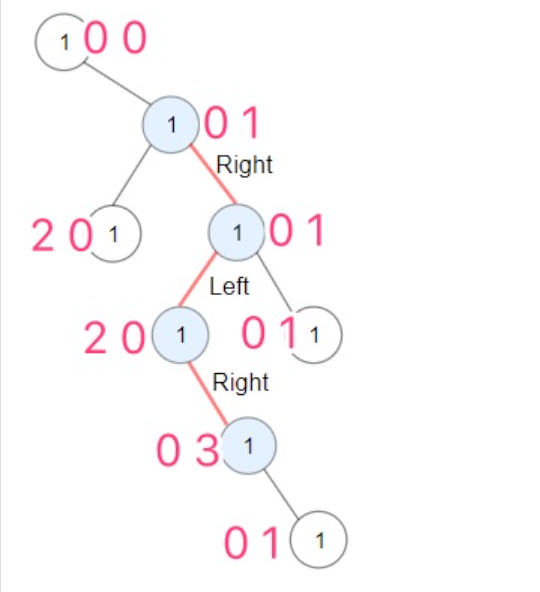
以题目中的树为例,第一个节点,l和r都为0.因为没有到达它的路径。
到第一个右节点时,因为它是右节点,所以它取父节点的l值加1,该节点的值就是 l = 0; r = 1;
它的左子树, 取它的r值,所以值为 l = 2, r = 0;
它的右子树,取它的l值,所以值为 l = 0, r = 1;
以依类推,我们就可以遍历出所有节点上面l和r值。
最终通过维护一个最大值来打擂台既可。
我觉得关键还是下面这句话:
这个可行在于,一个节点没办法被父节点既选择向左又选择向右,要么跟随父节点向左,那就+1,要么自己向右,那就从0开始,反之亦然











