深度学习与神经网络 | 邱锡鹏 | 第五章学习笔记 卷积神经网络
五、卷积神经网络
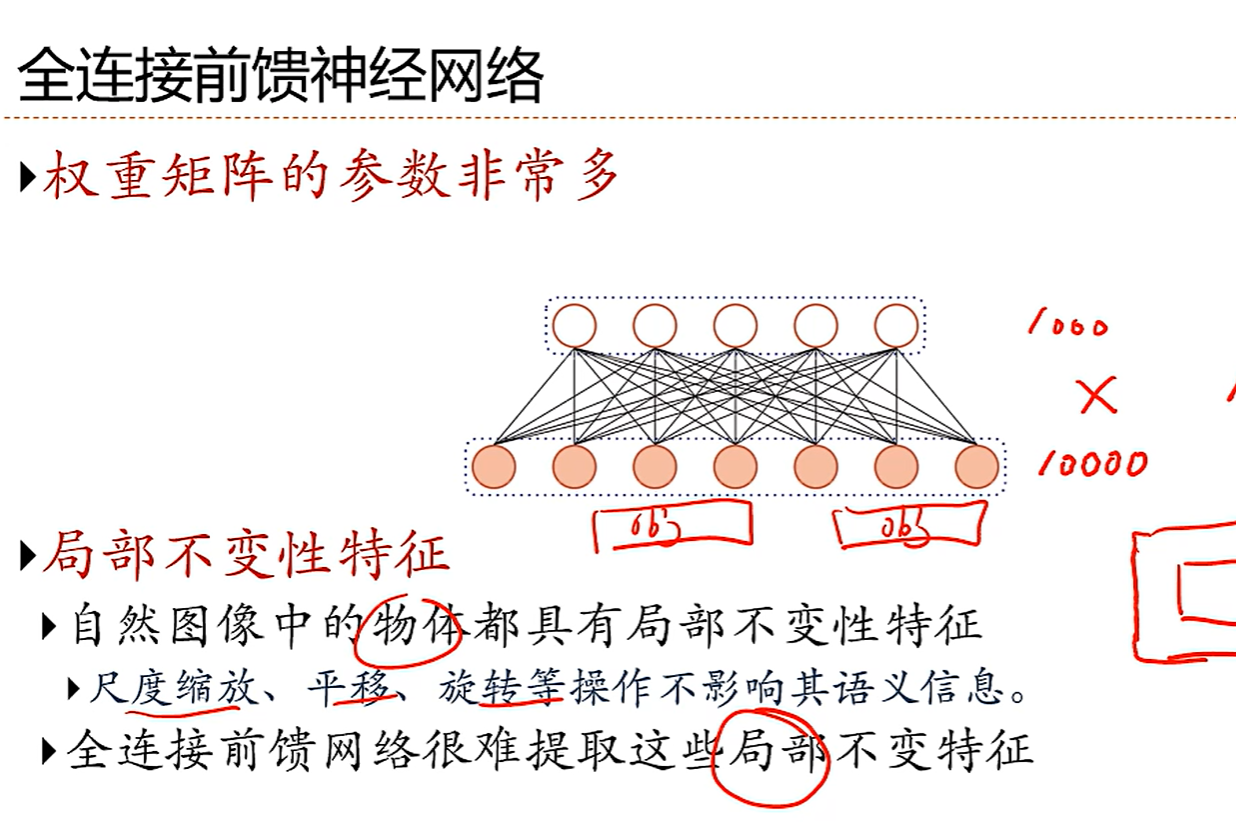
我们希望有一个新的网络可以提取局部不变性
5.1 卷积
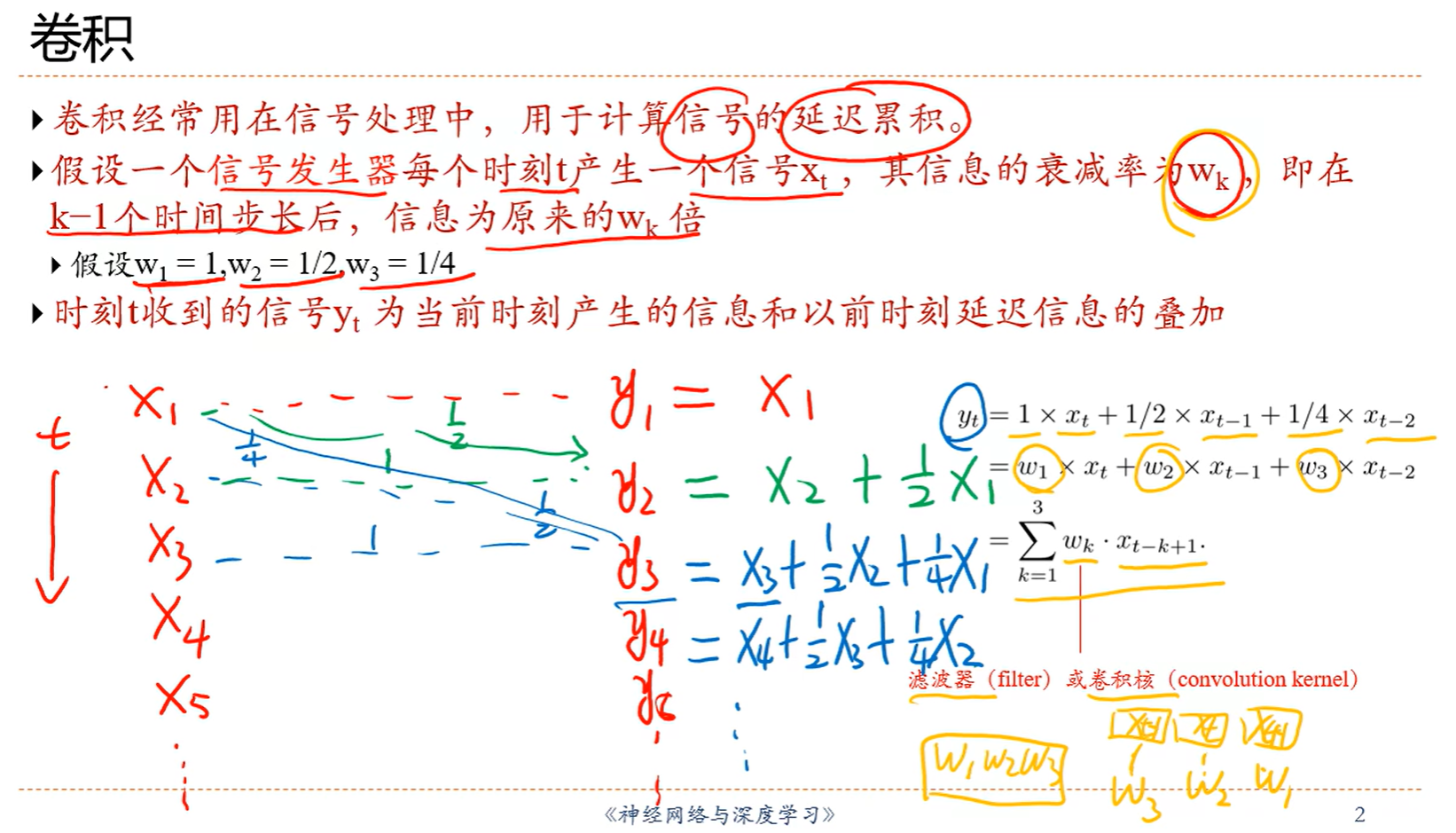
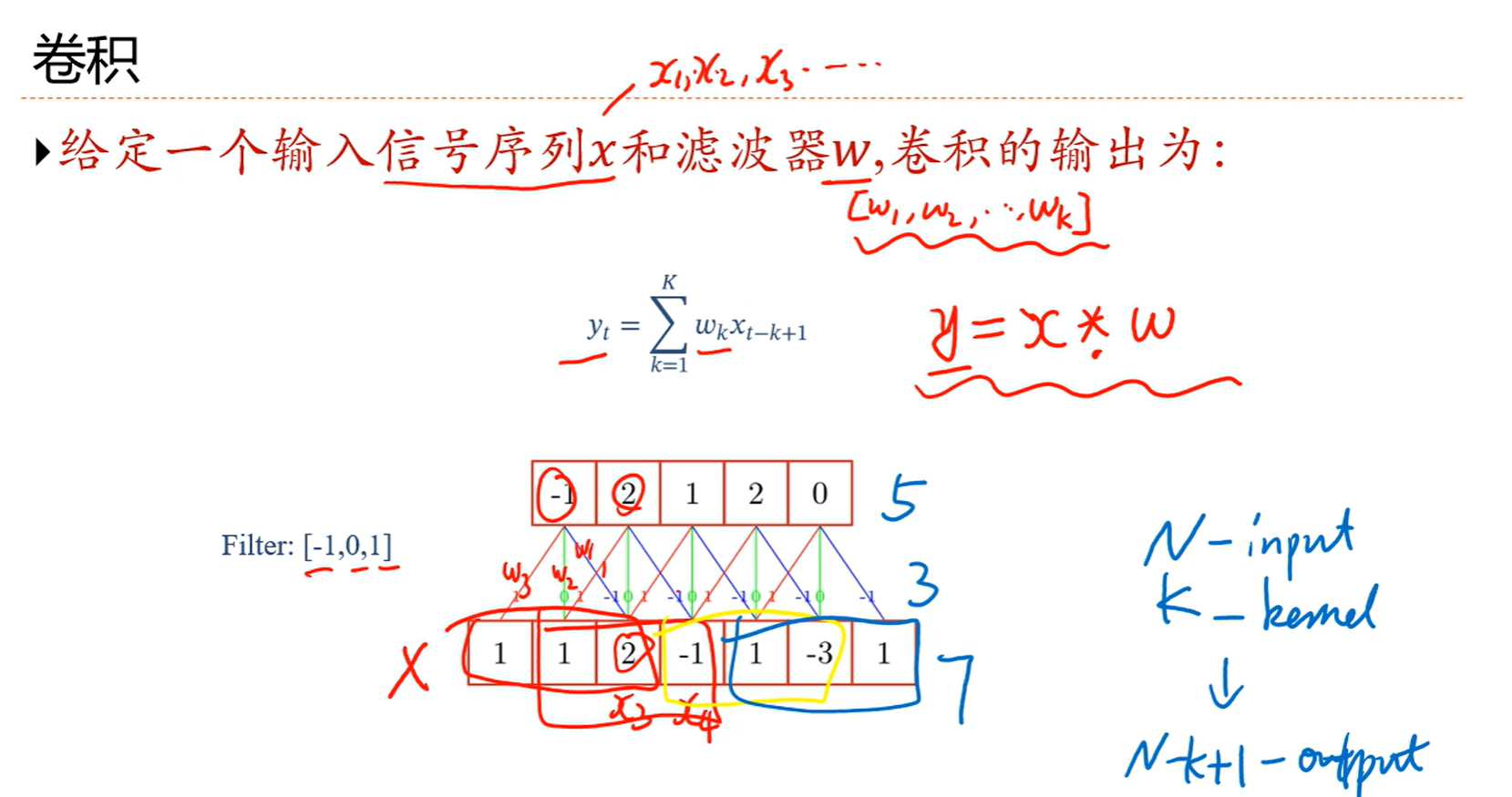
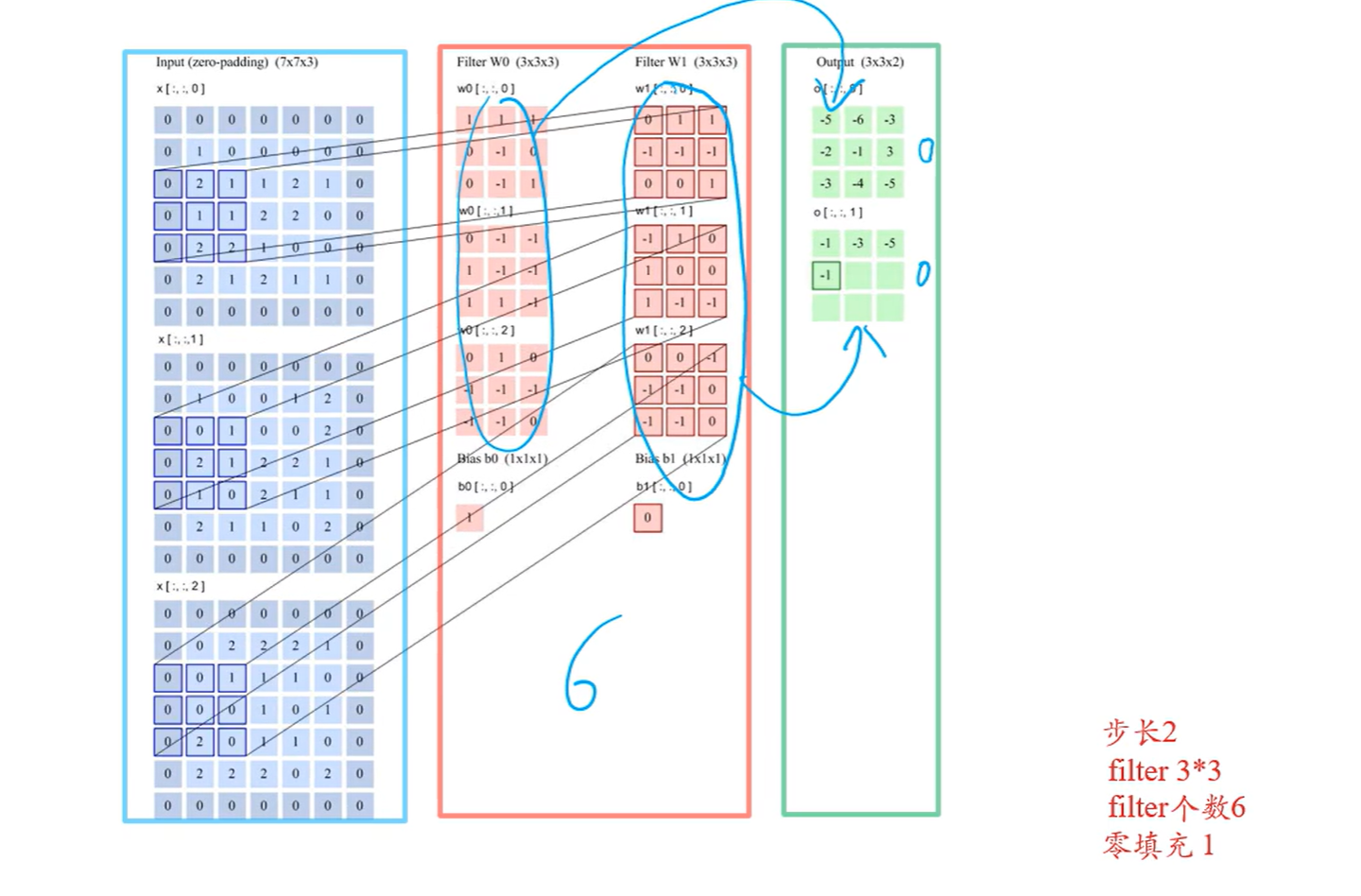
前两个输入都不卷,从第三个开始卷,因为滤波器的长度是3
每次选定三个数卷,比如前三个,1,1,2
2* (-1) + 1*0+1*1= -1
然后根据公式就是如上计算,就是滤波器的第三个对应当前选定的三个值的第一个,第二个对第二个,第一个对第三个,其实就是倒着来的,后面的也都是如此
然后可以看到,输入有7个,输出有5个,滤波器大小是3,那么关系就是7-3+1=5
也就是n-k+1=5

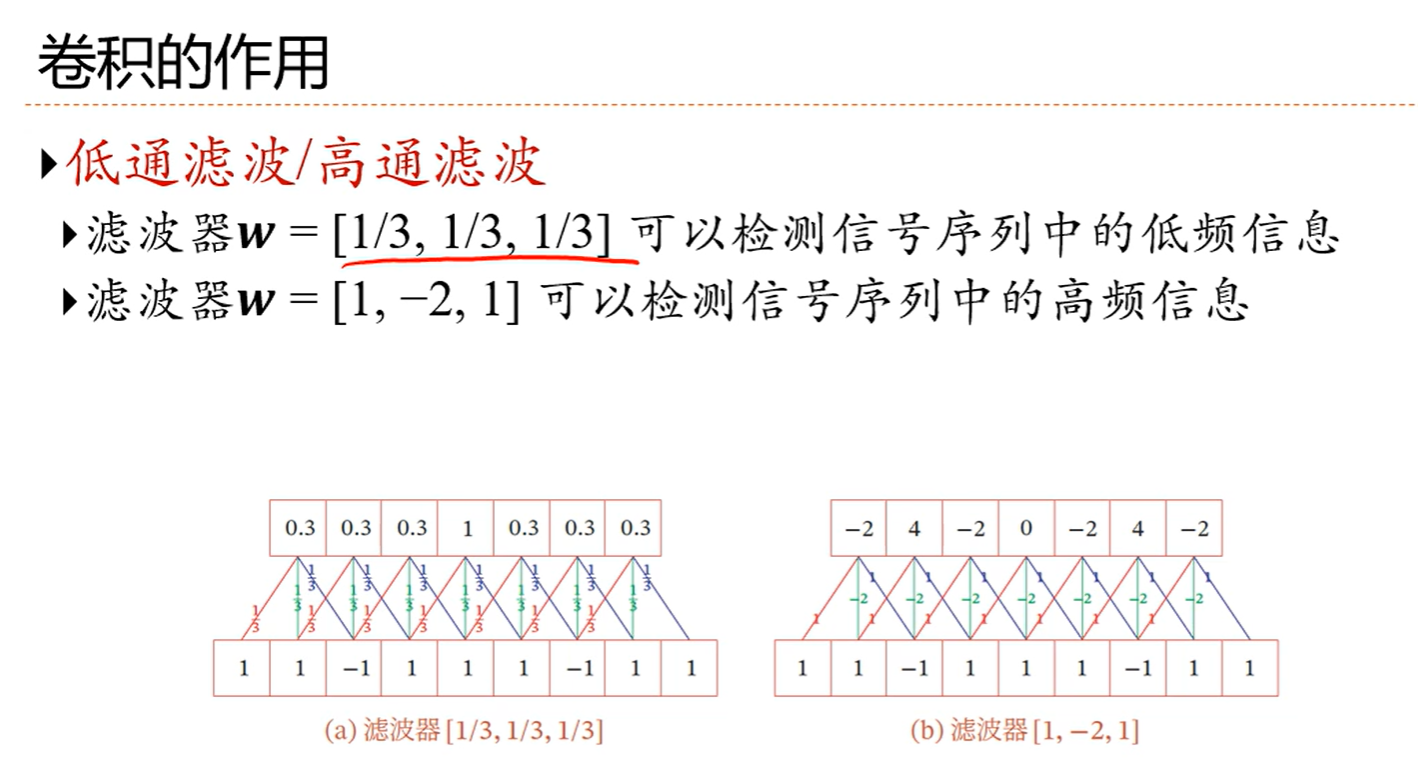
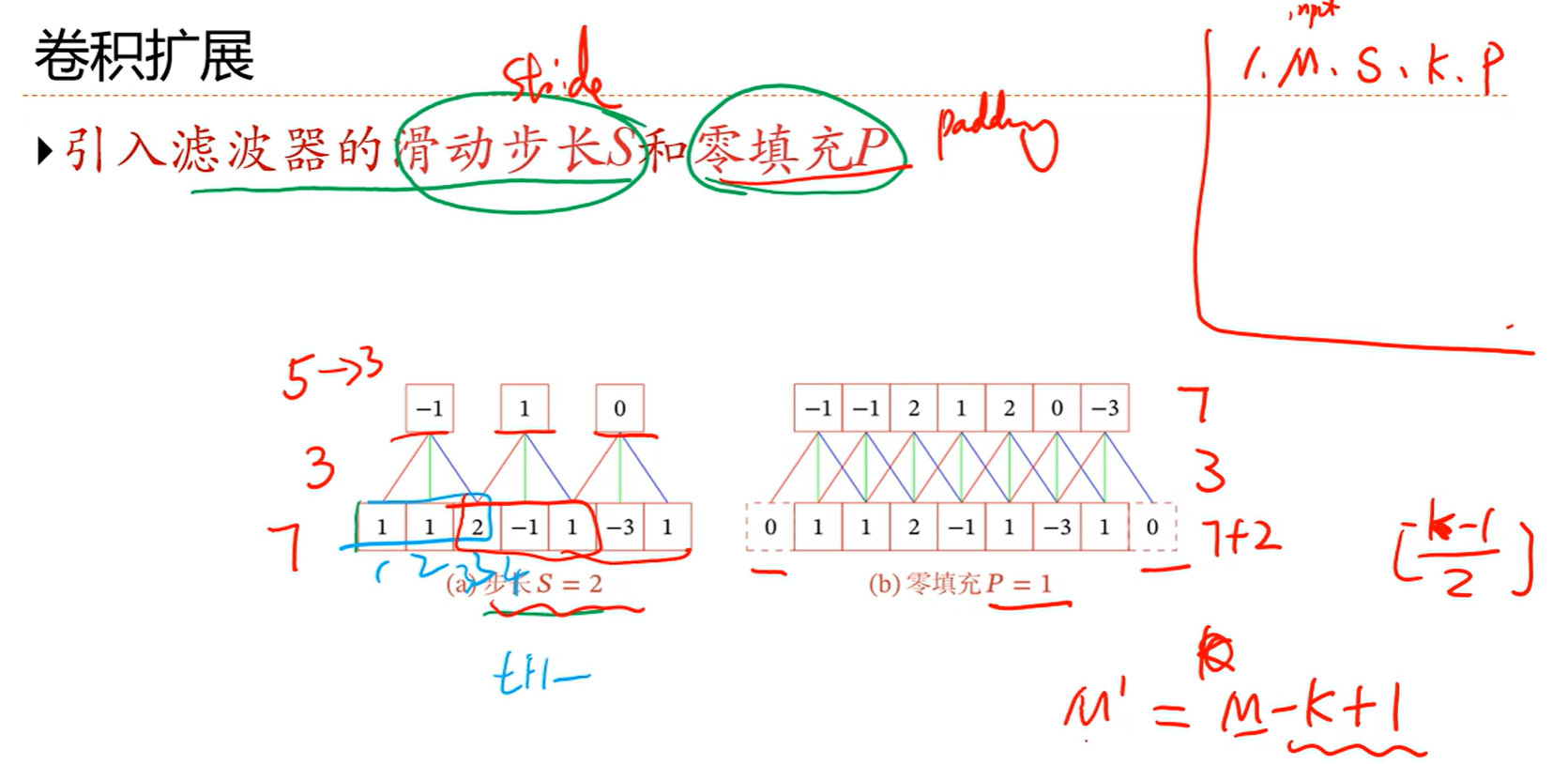
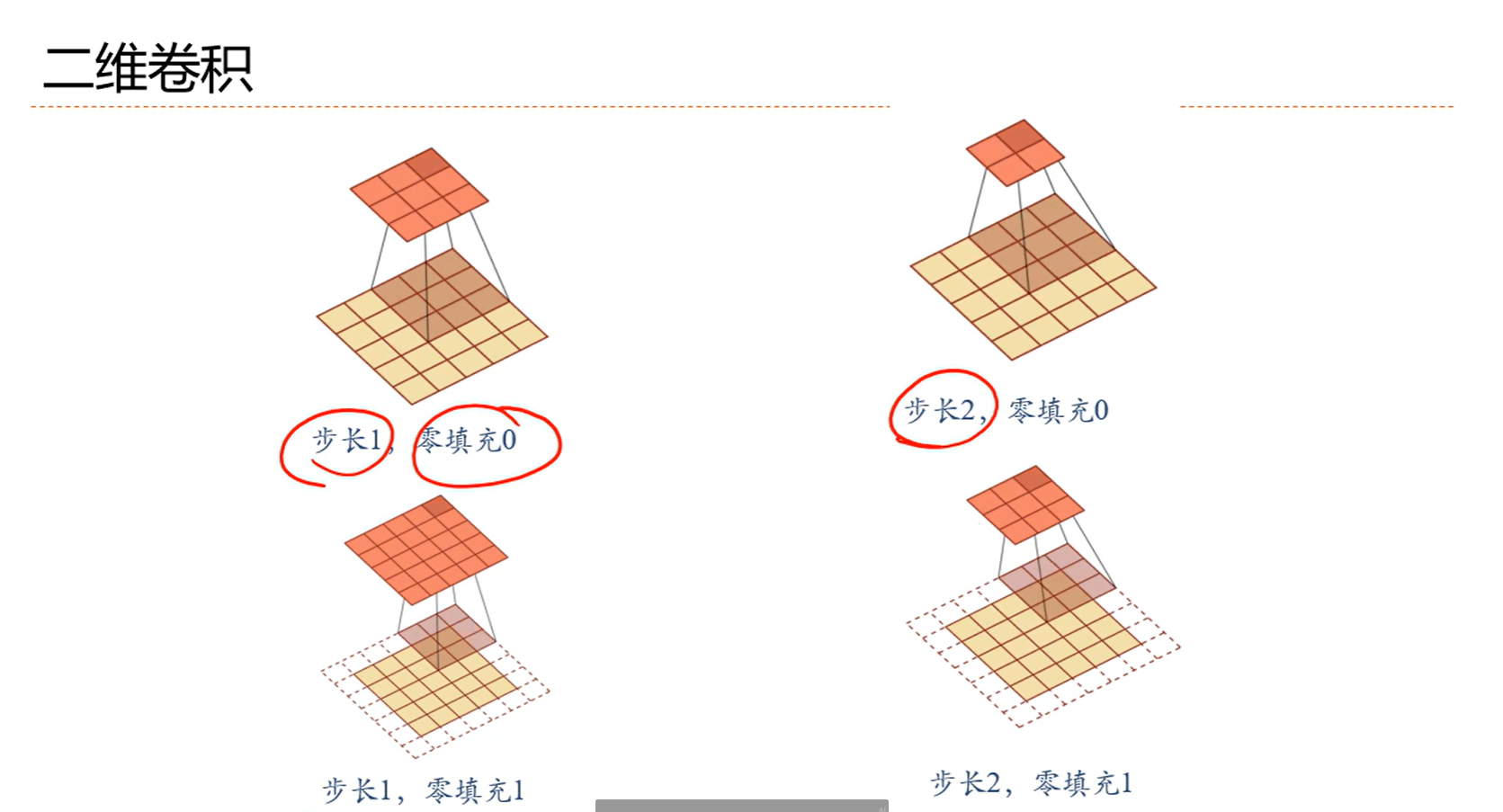
零填充很常用,因为这个可以让输入和输出长度相同
比如图中输入是7,滤波器是3,输出本来应该是5,现在零填空P=1,那就是补了两个零,表面上输入好像成9了,这么一算,输出就是7,但实际上输入还是原来的7,因为那两个0是补进去的
其实P=(k-1)/2,也就是输入会补k-1个0

5-3+1=3,依旧满足上面那个规则
5.2 卷积神经网络
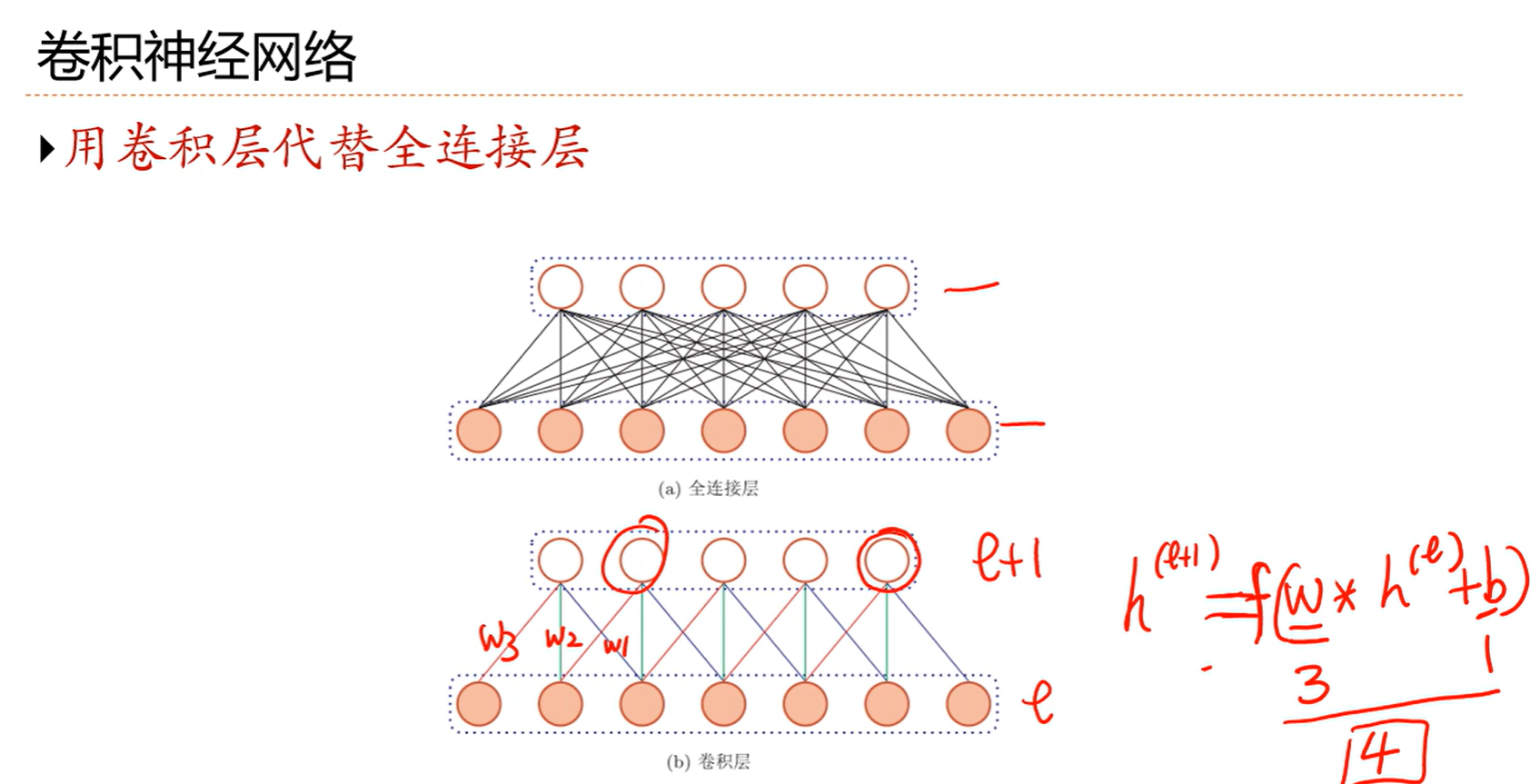
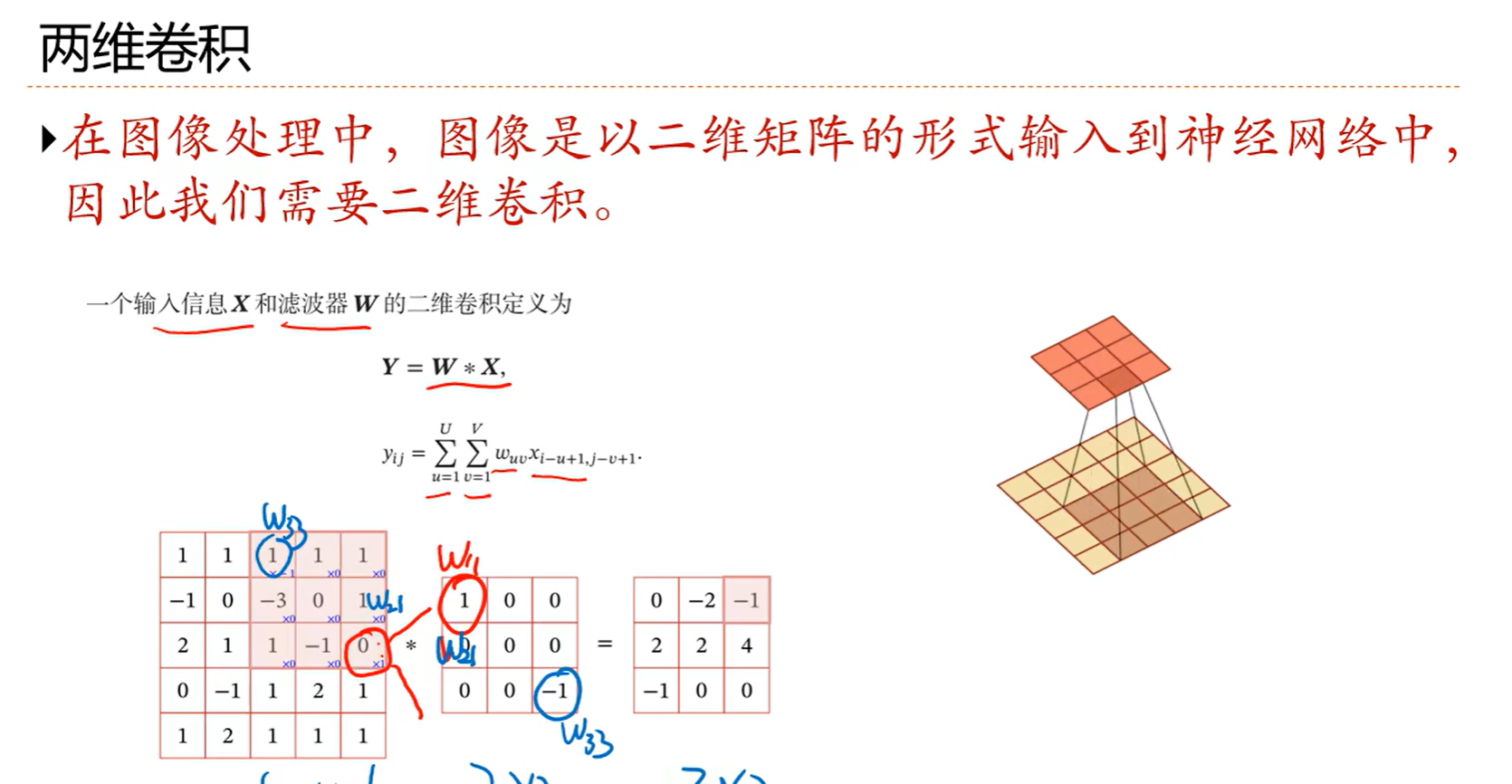
用卷积核代替全连接,原来每个连接都是一个参数,现在换成卷积核,这里卷积核是3(滤波器大小),所以参数也就是3个,再加上一个偏置b,一共是4个,偏置也是共享的
而且这个参数数量和输入的神经元数量无关
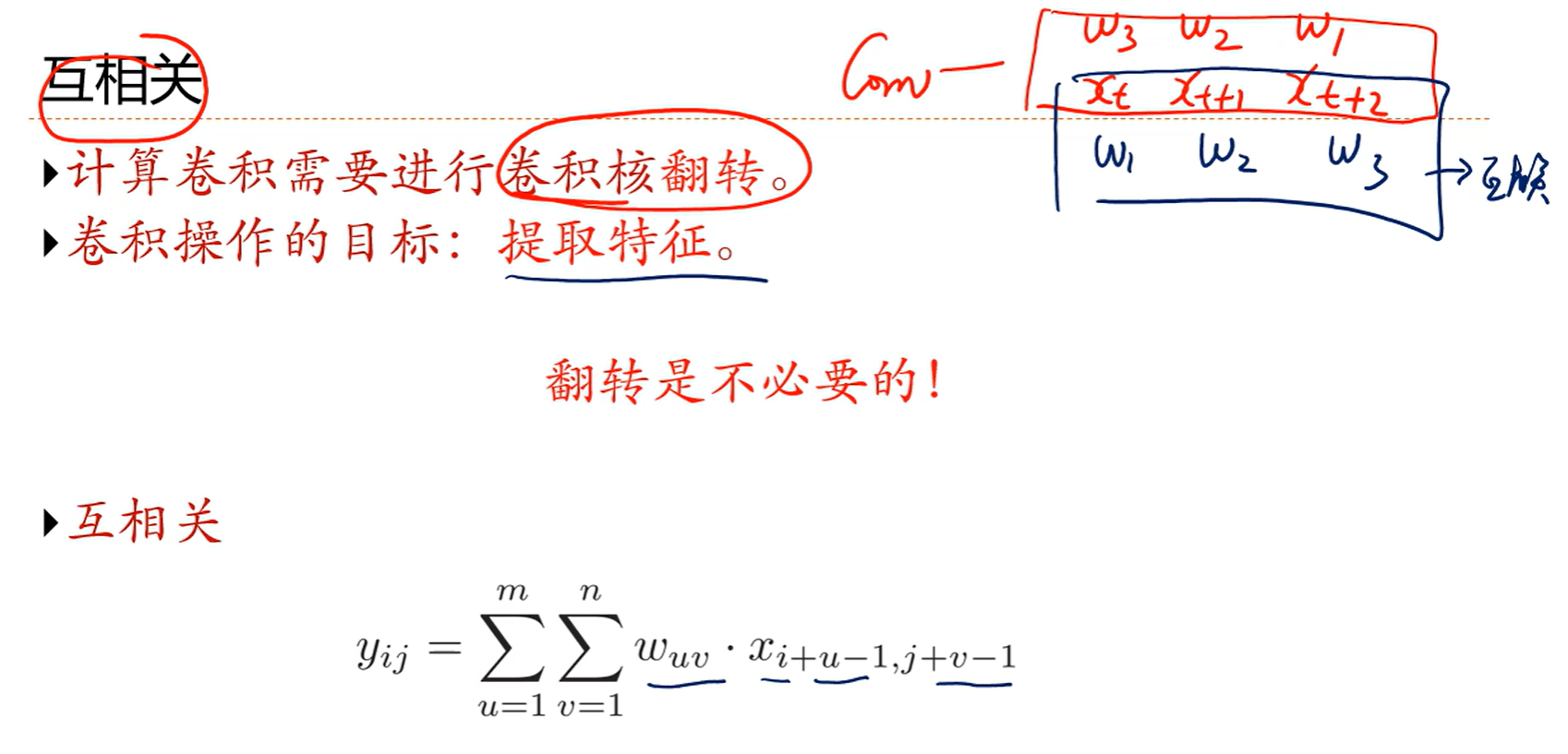
不反着来正着来就是互相关,即w1对x1,w2对x2,一般不做特殊说明就是互相关
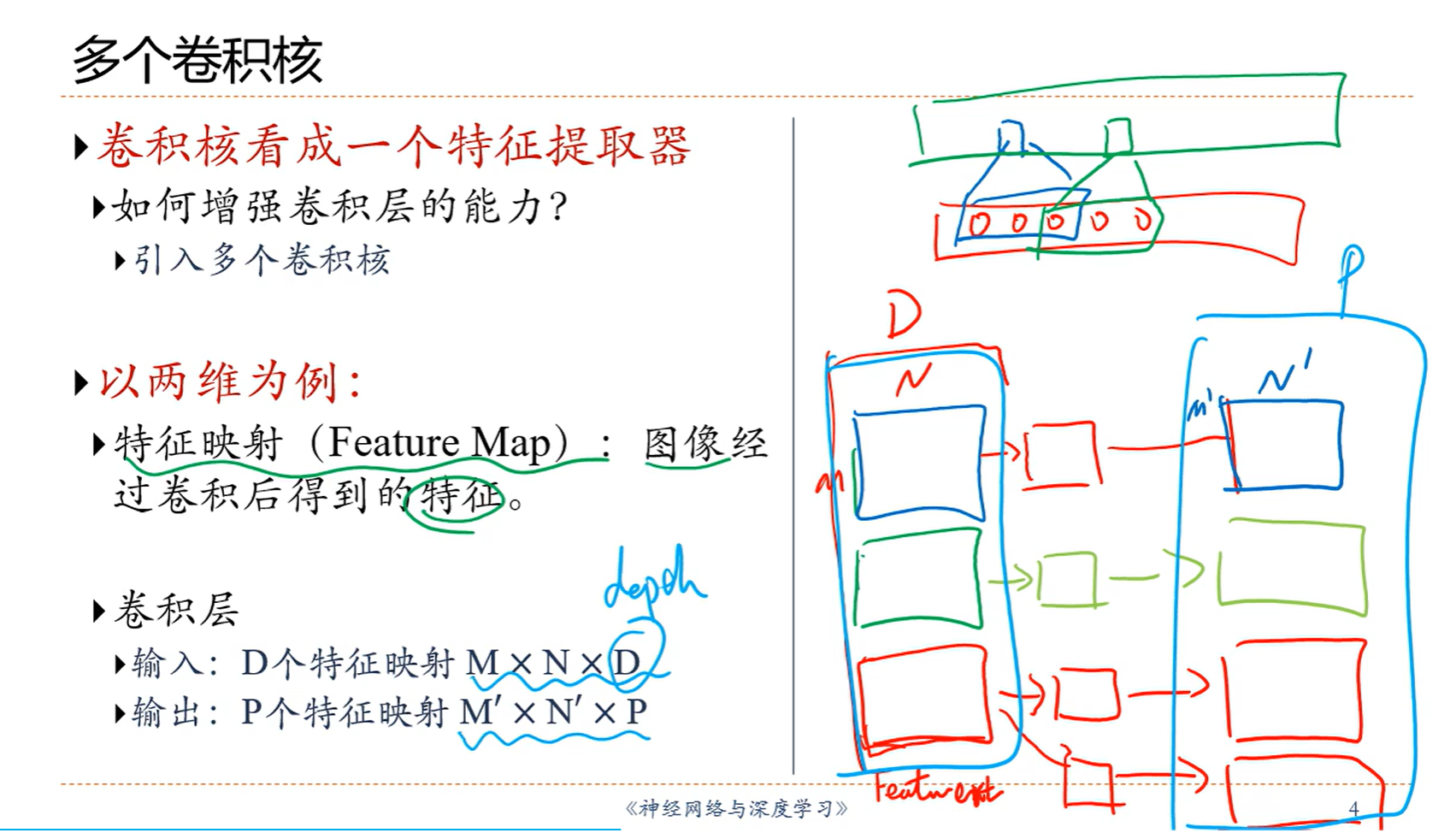
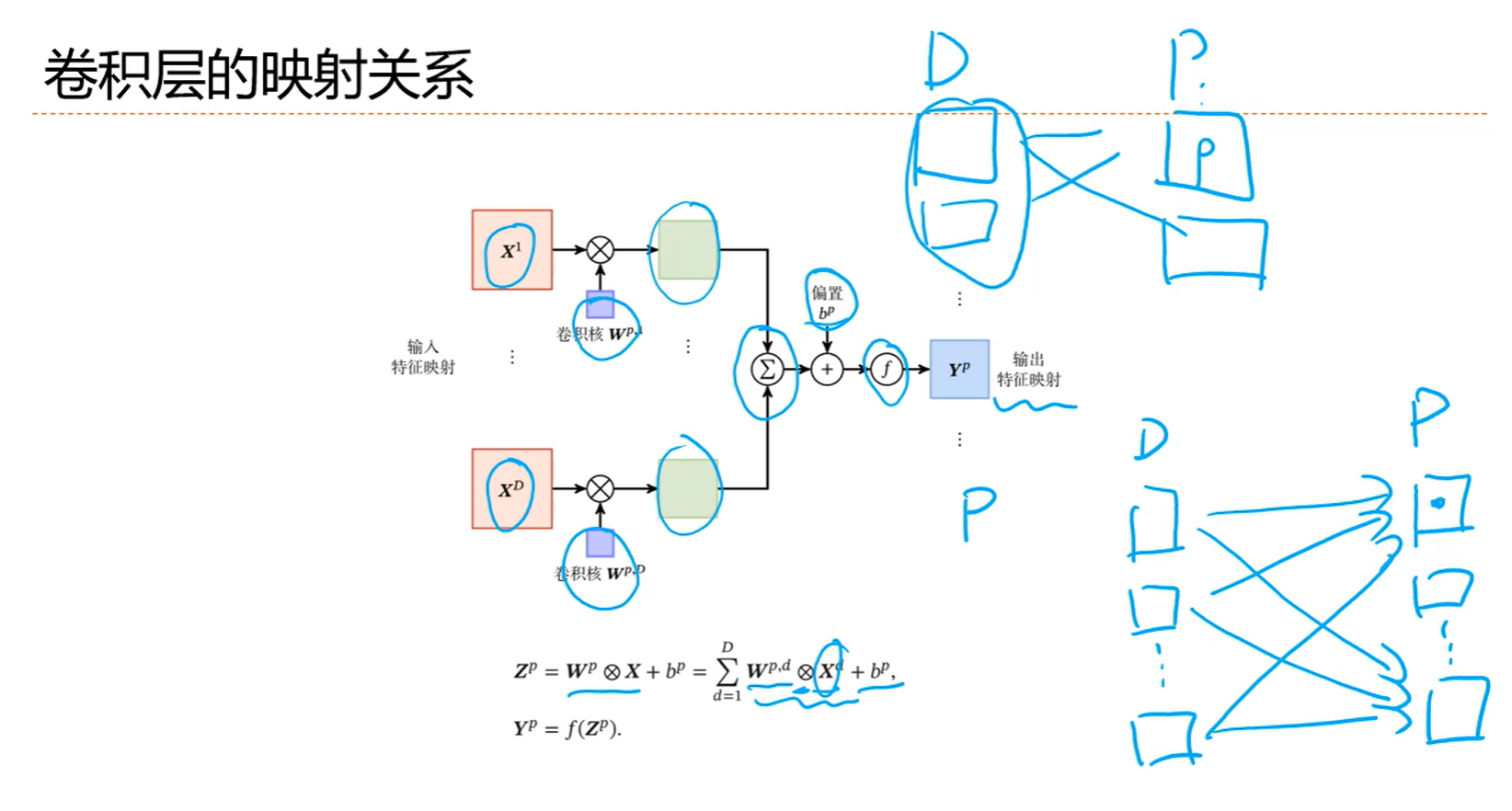
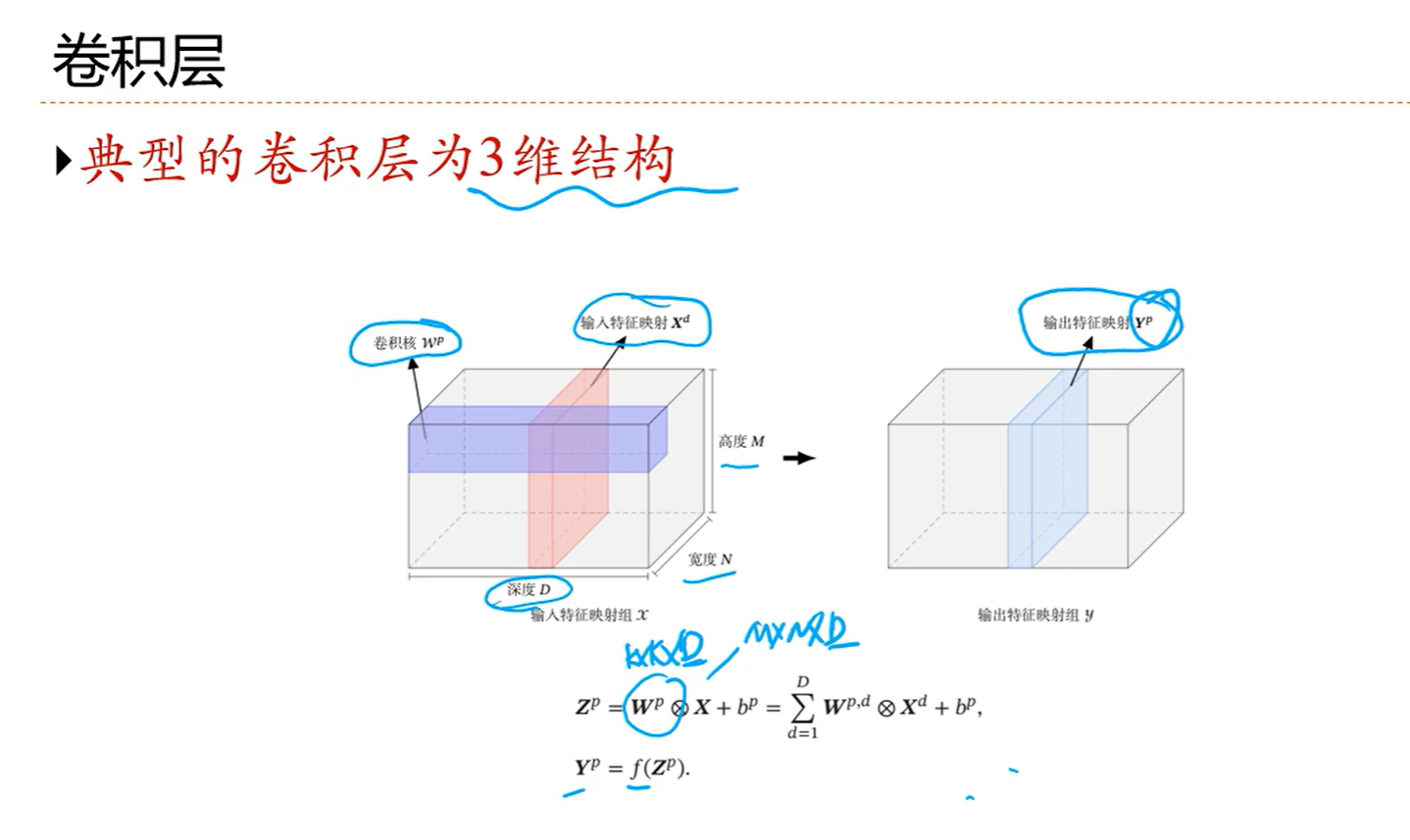
D就是通道数,在右边这张图里面就是3,MN是原来的大小
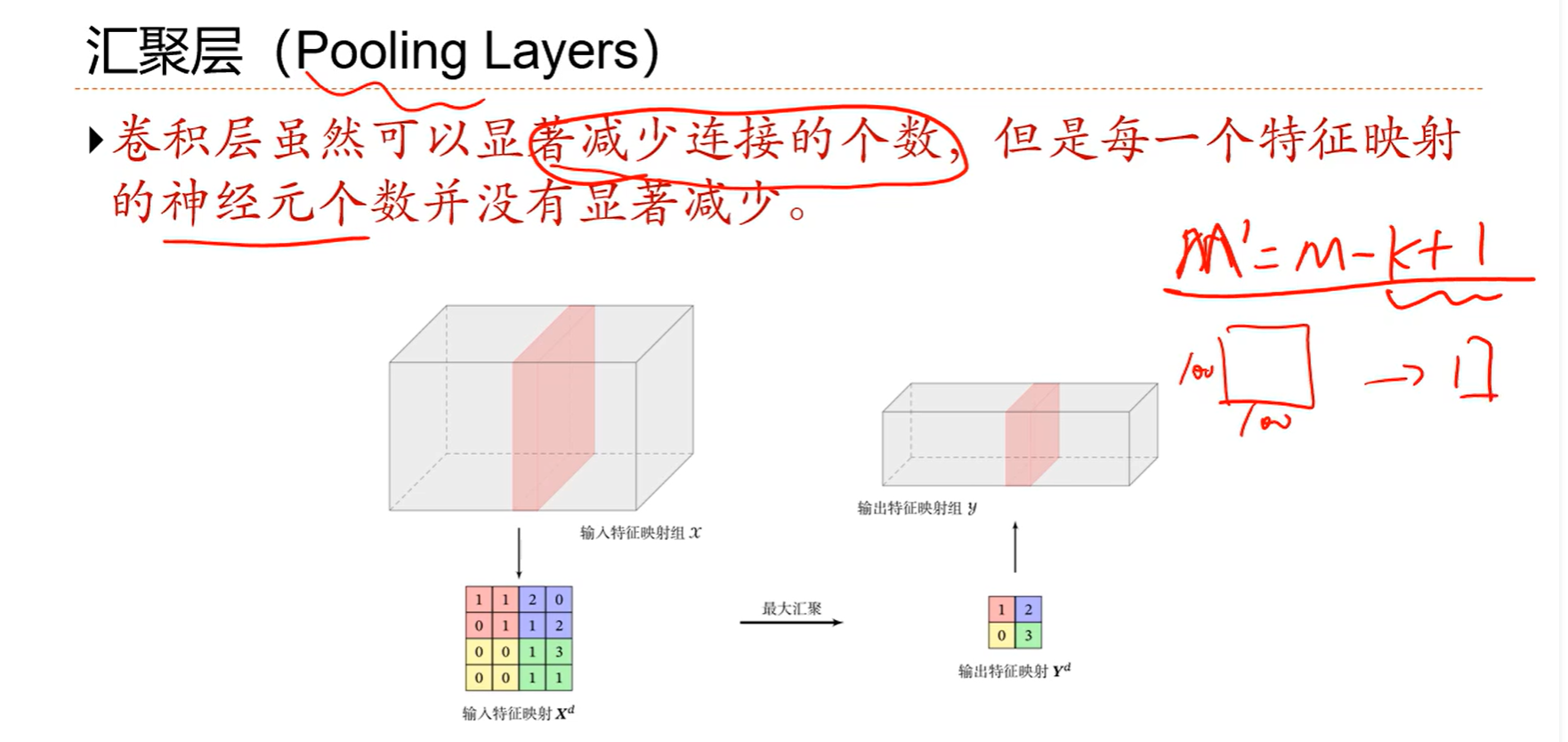
划分成区域就可以显著降低神经元个数了,原来4*4变成了2*2
划分成4个互不相交的区域以后,怎么汇聚 可以是平均值或者最大值或者其他的规则
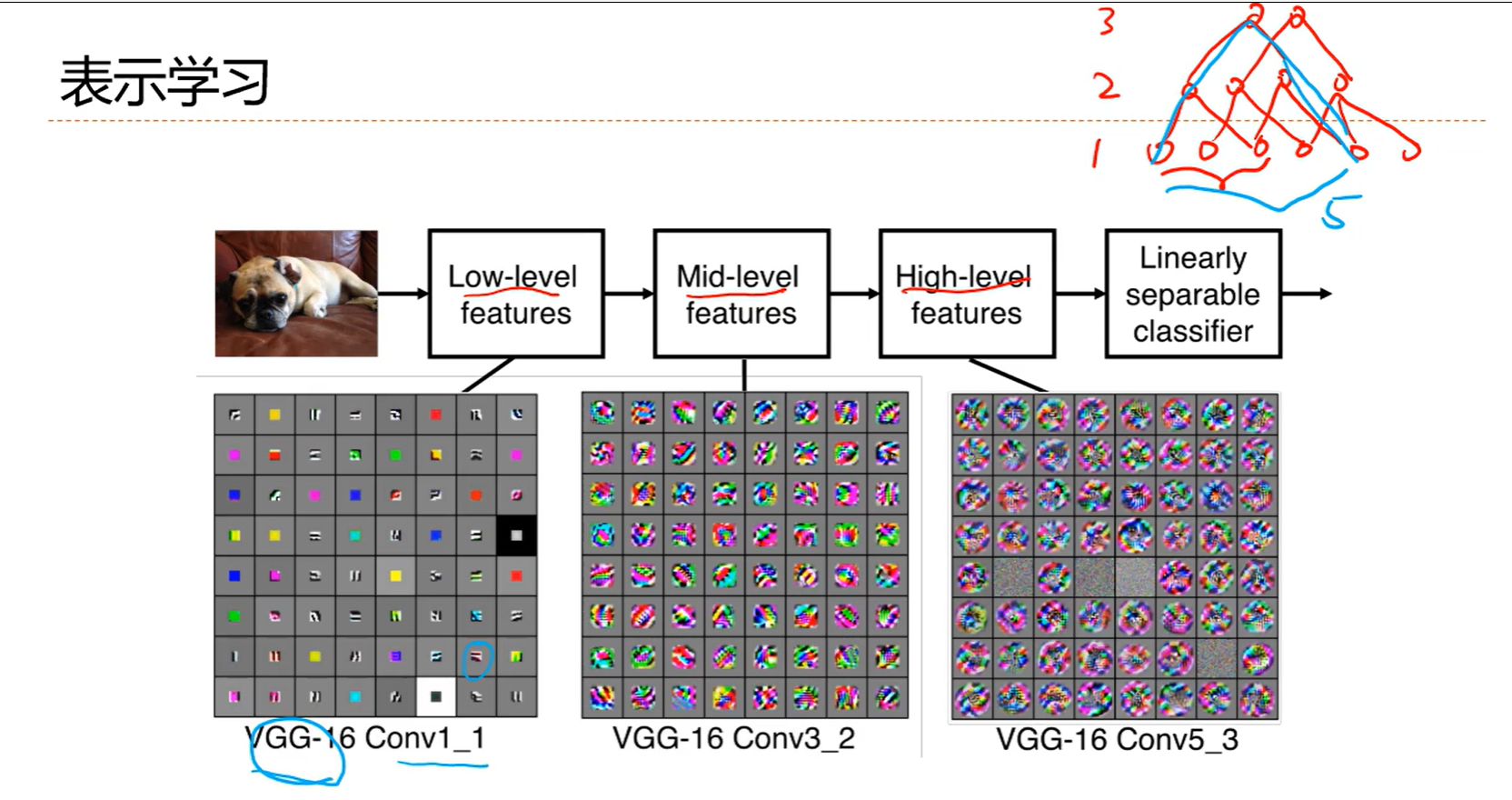
5.3 其他卷积
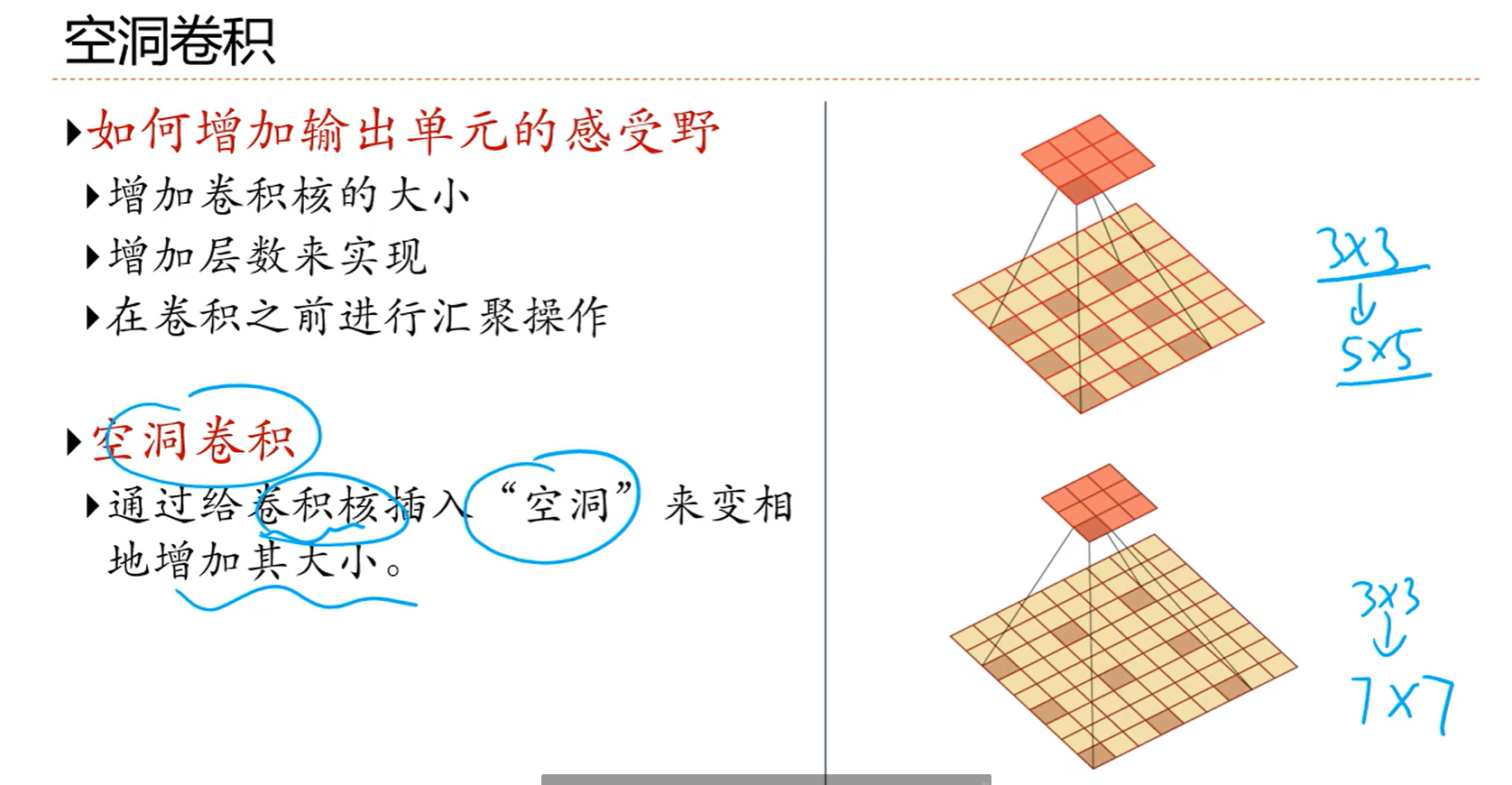
空洞其实就是插入0,把3*3弄成5*5的
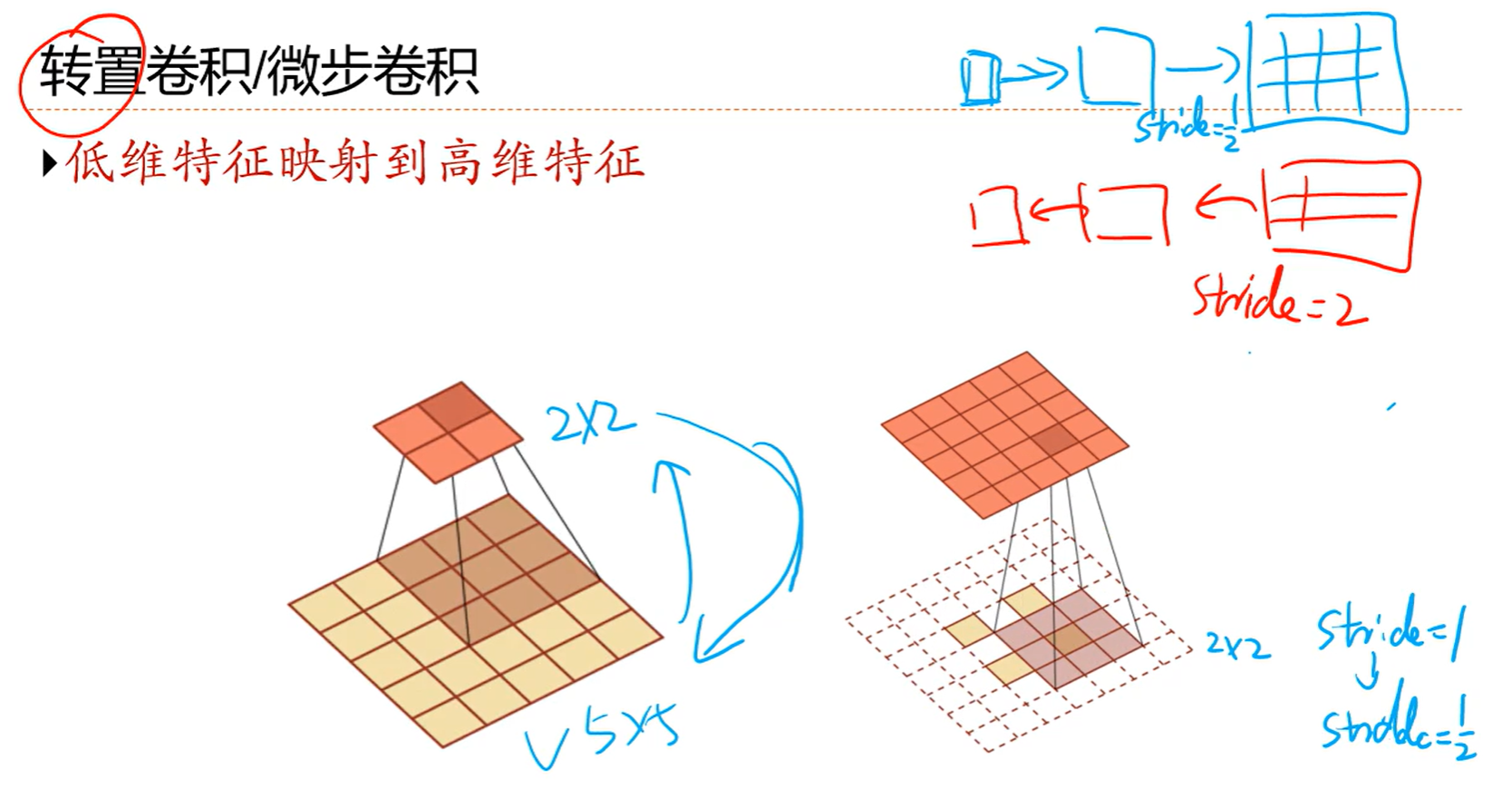
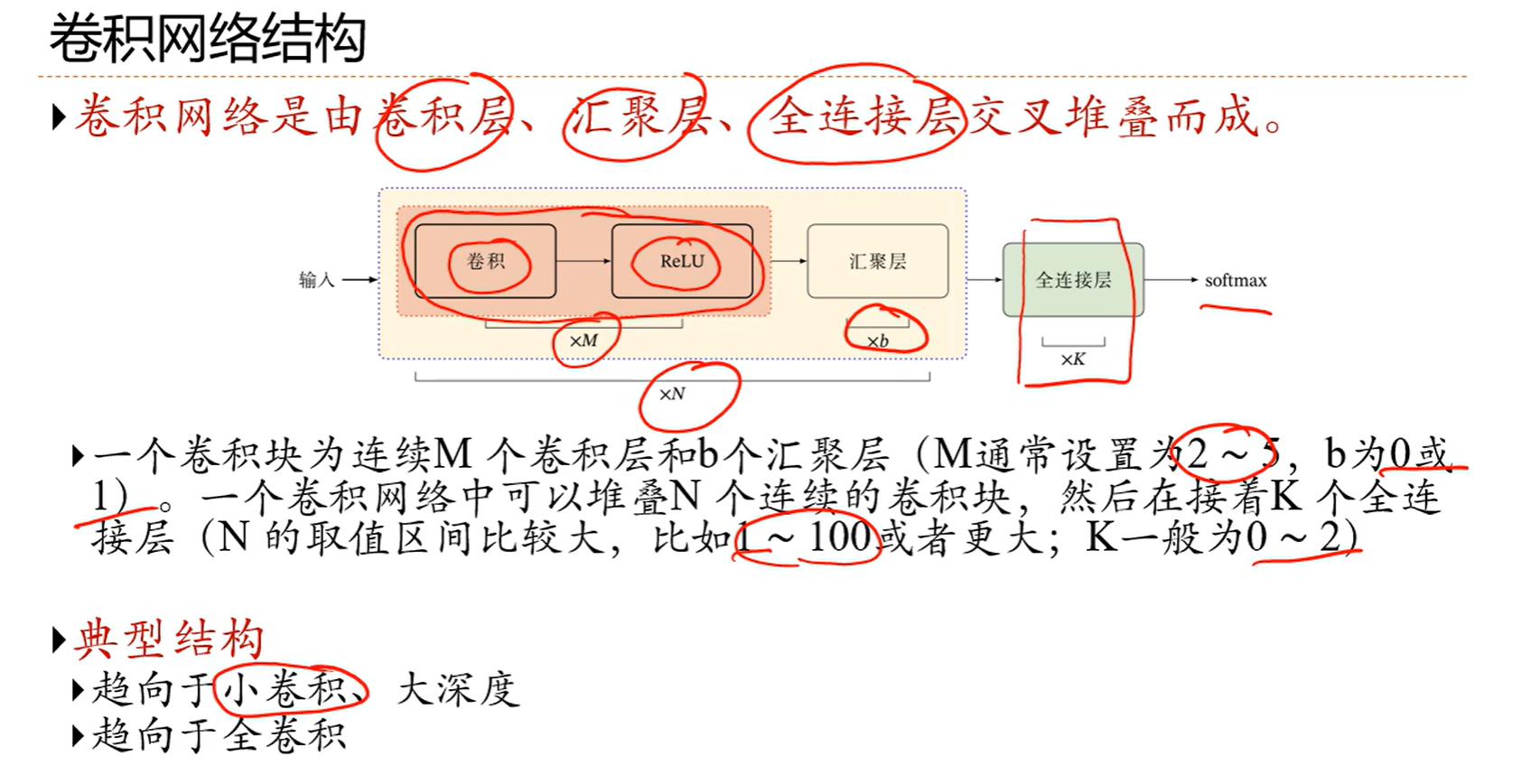
5.4 经典卷积网络
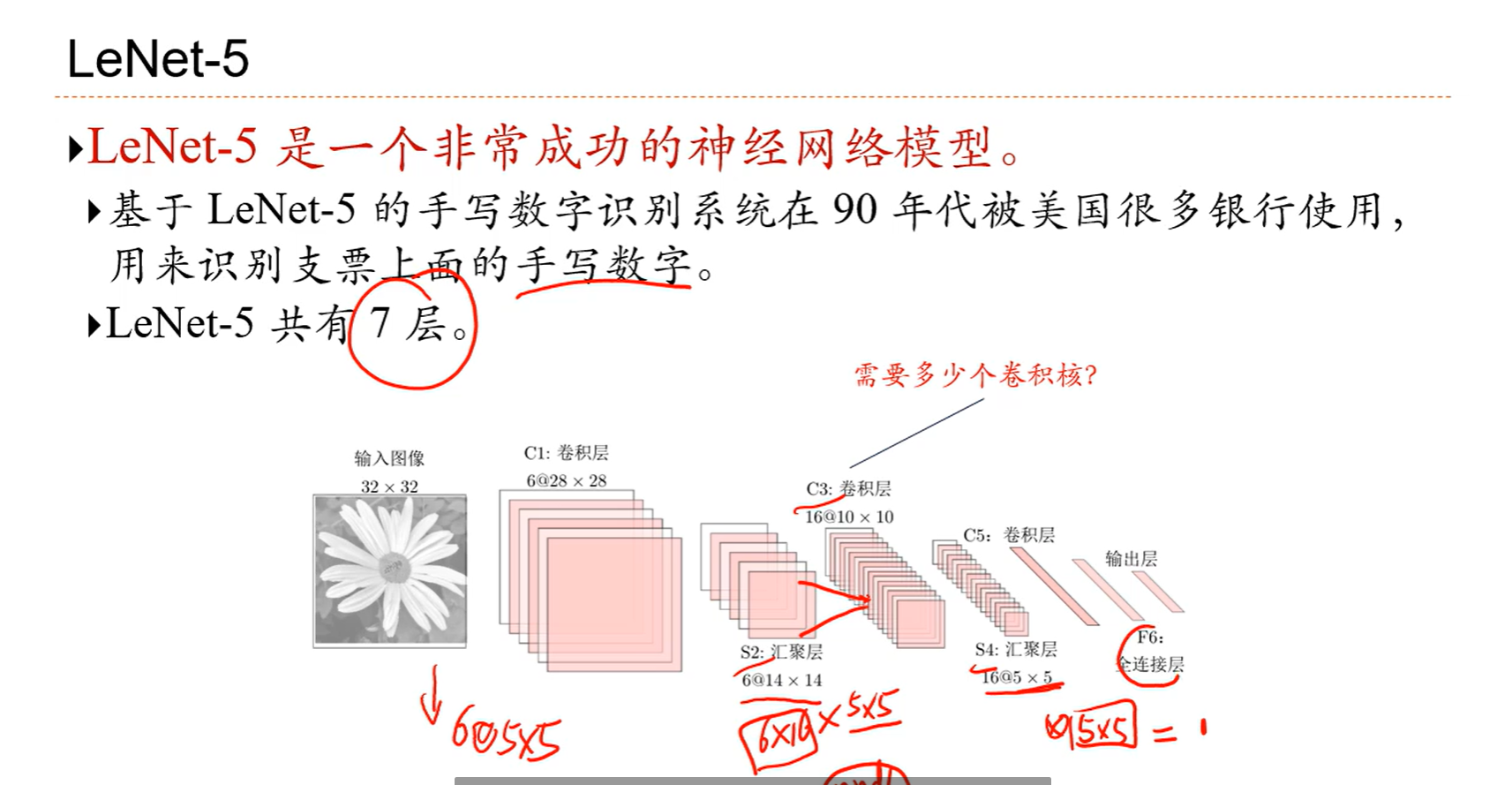
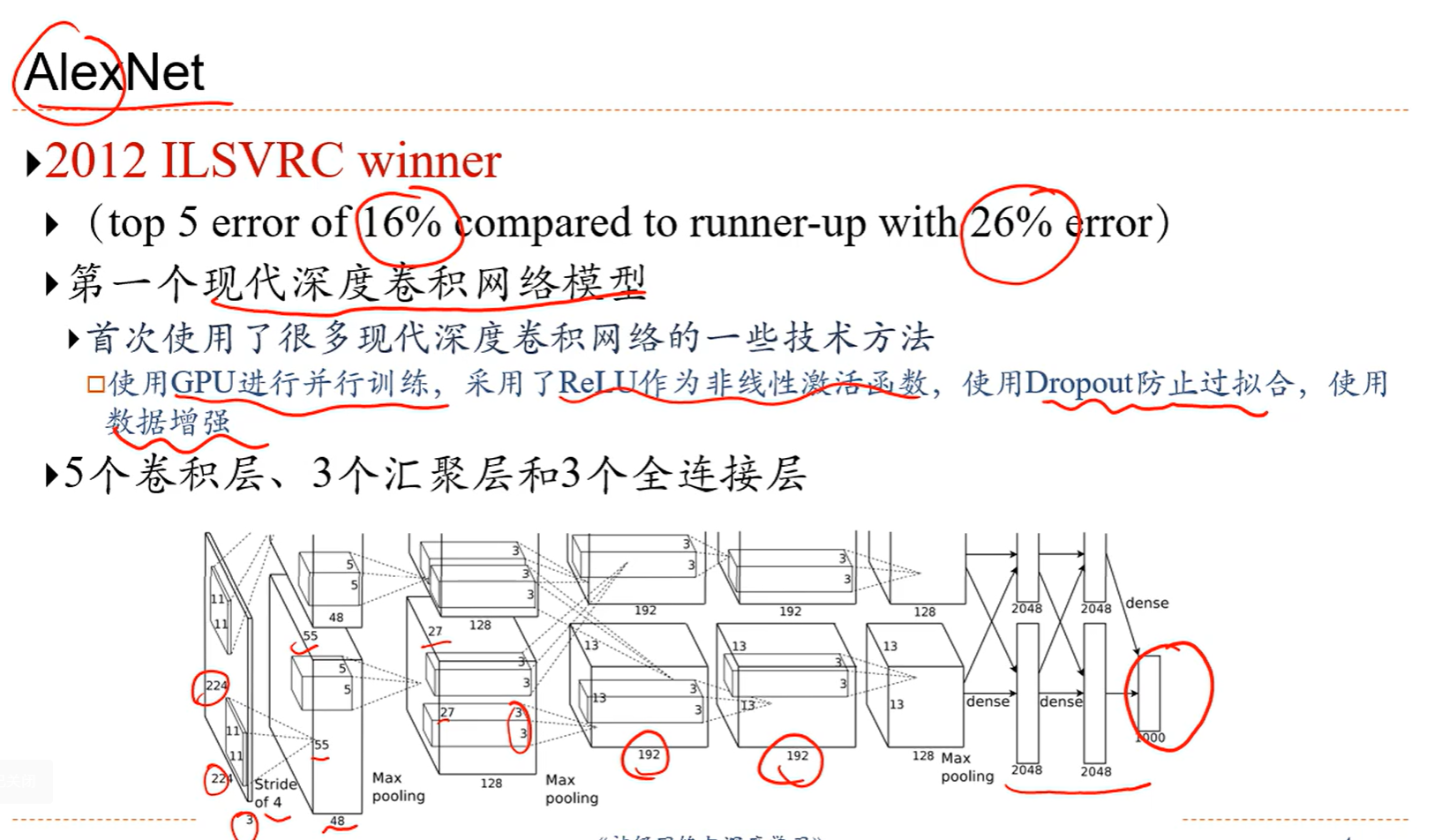
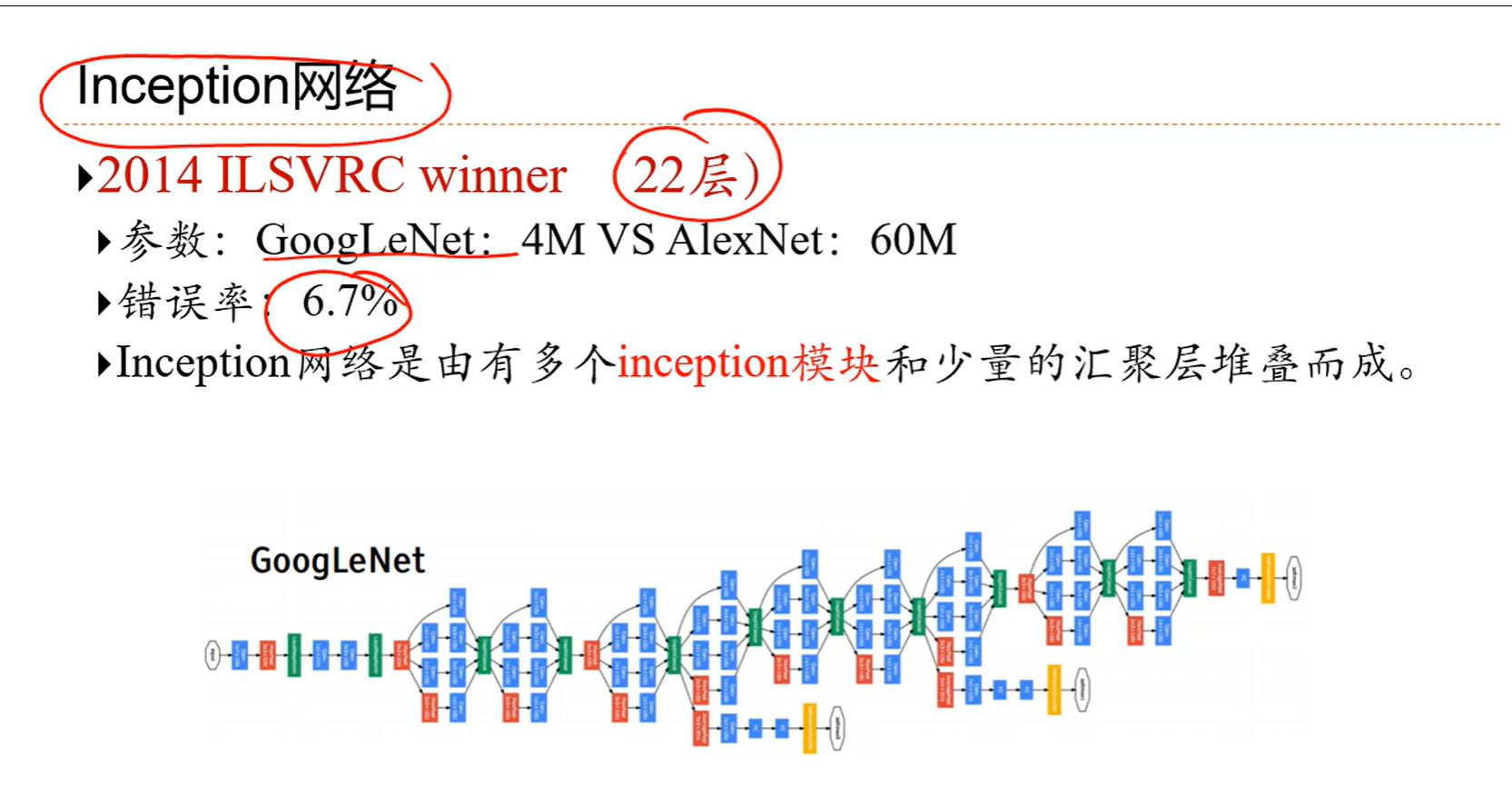
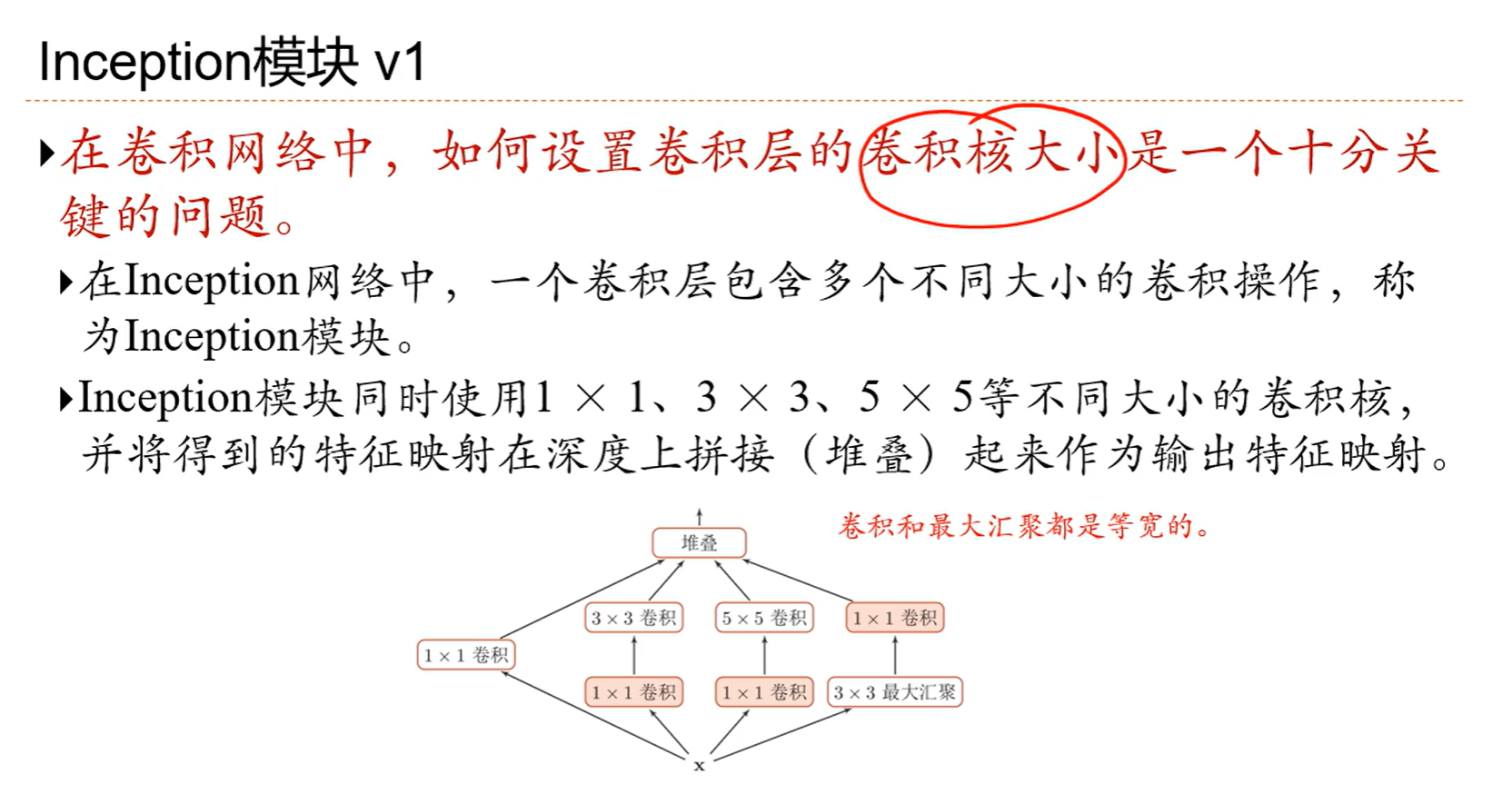
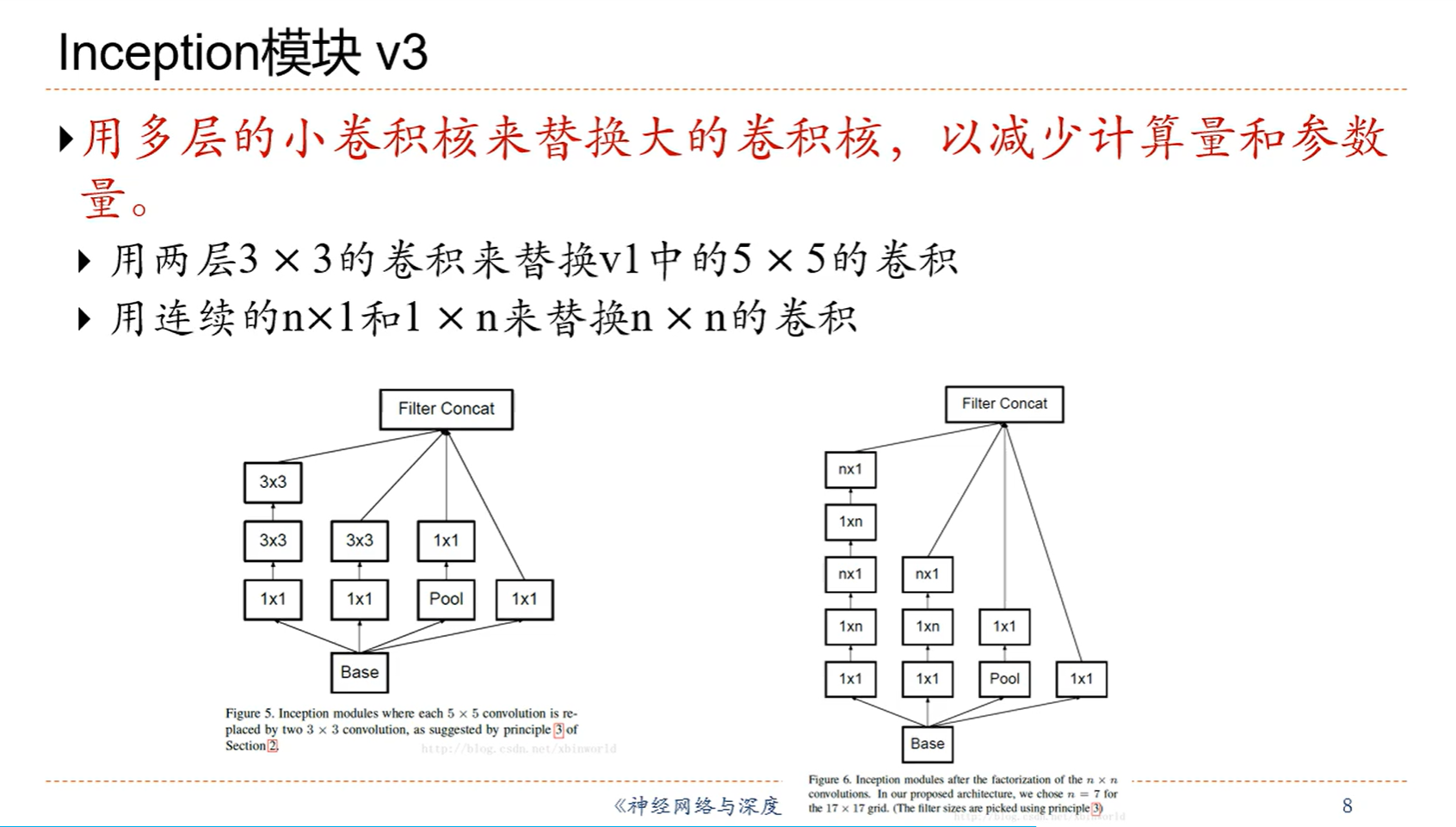
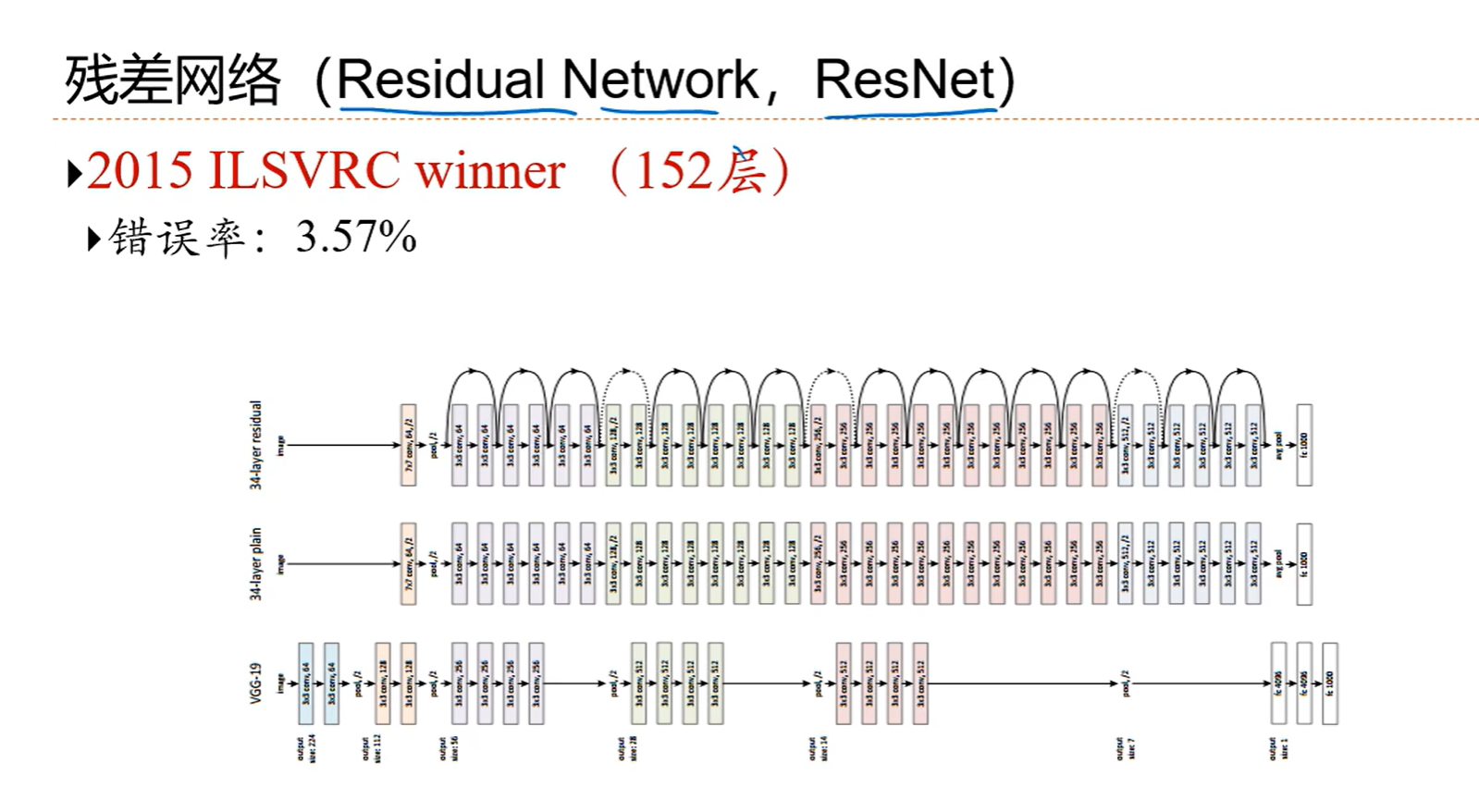

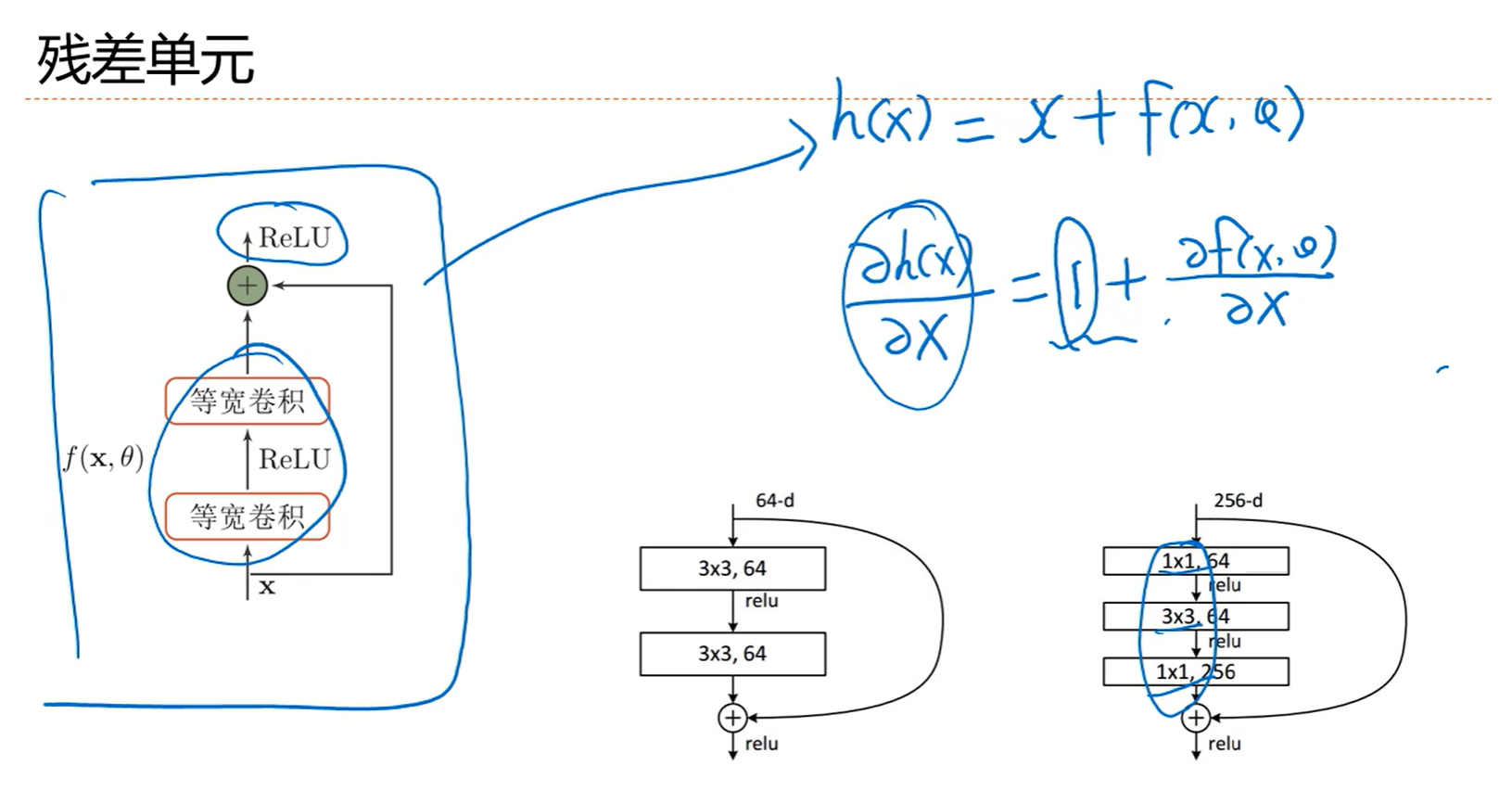
直连边会让求导会有一个恒等的1,也就是如果想让层数深的话,直接相连的边必不可少
5.5 卷积网络的应用

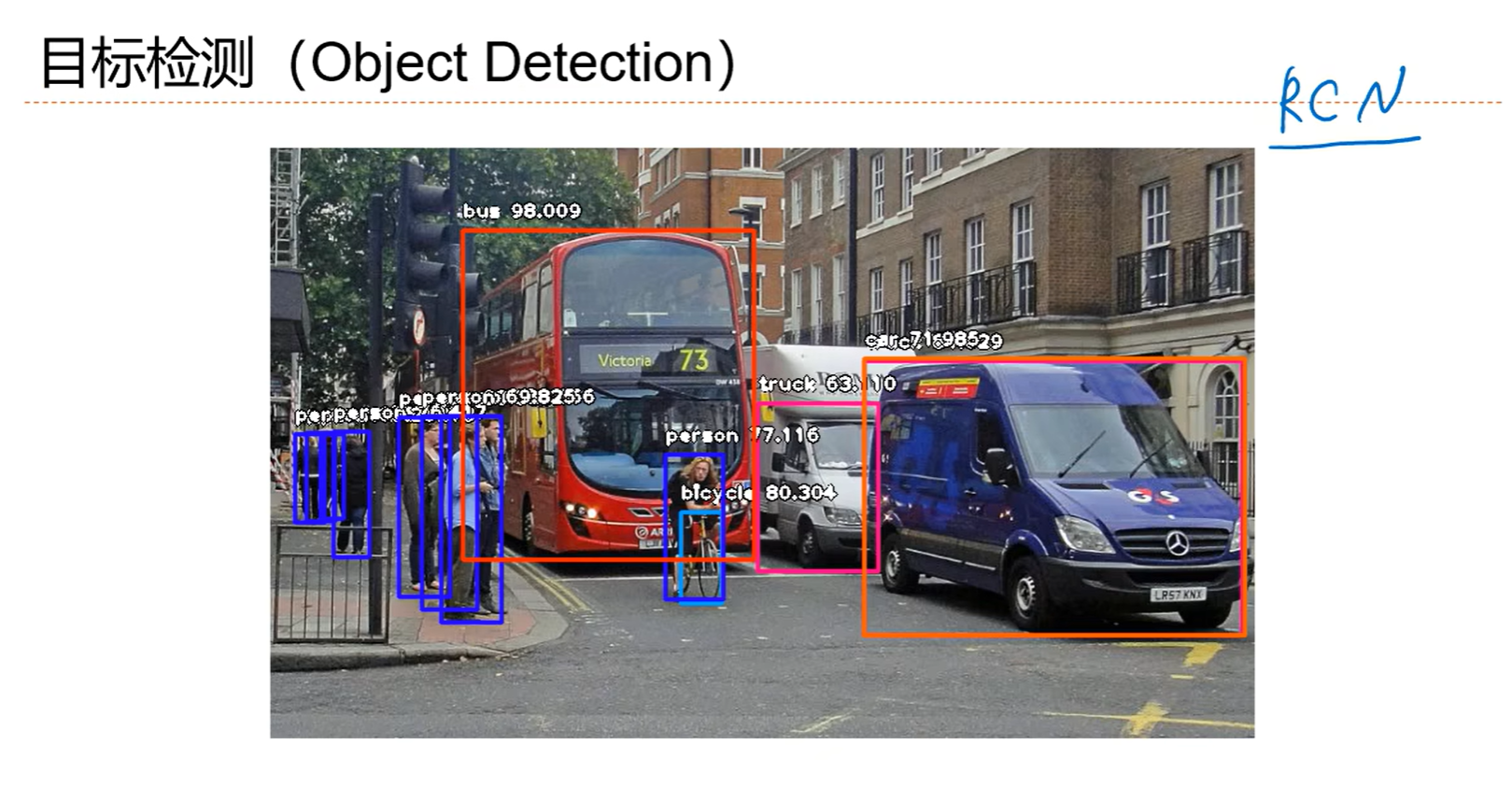


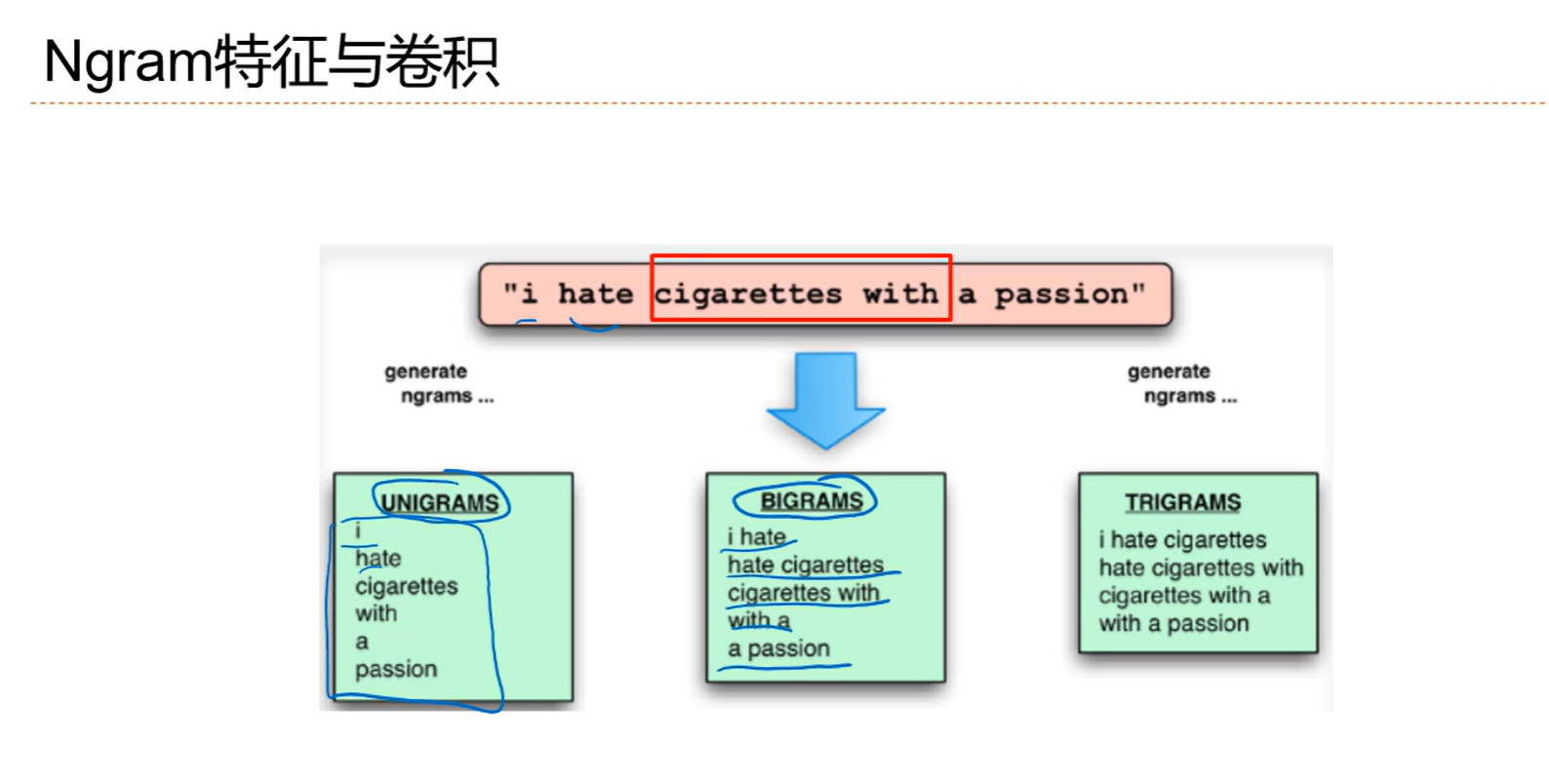
5.6 应用到文本数据
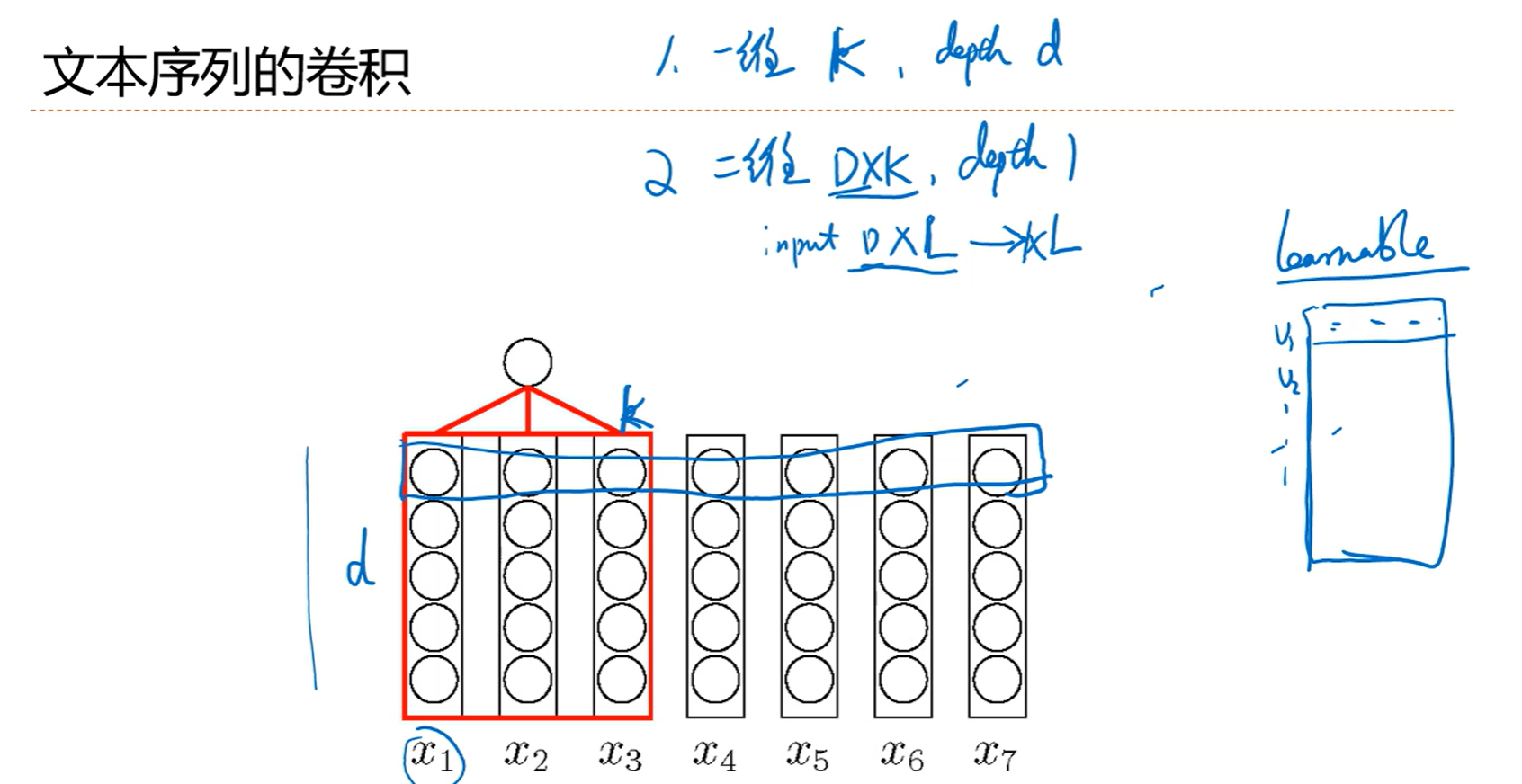
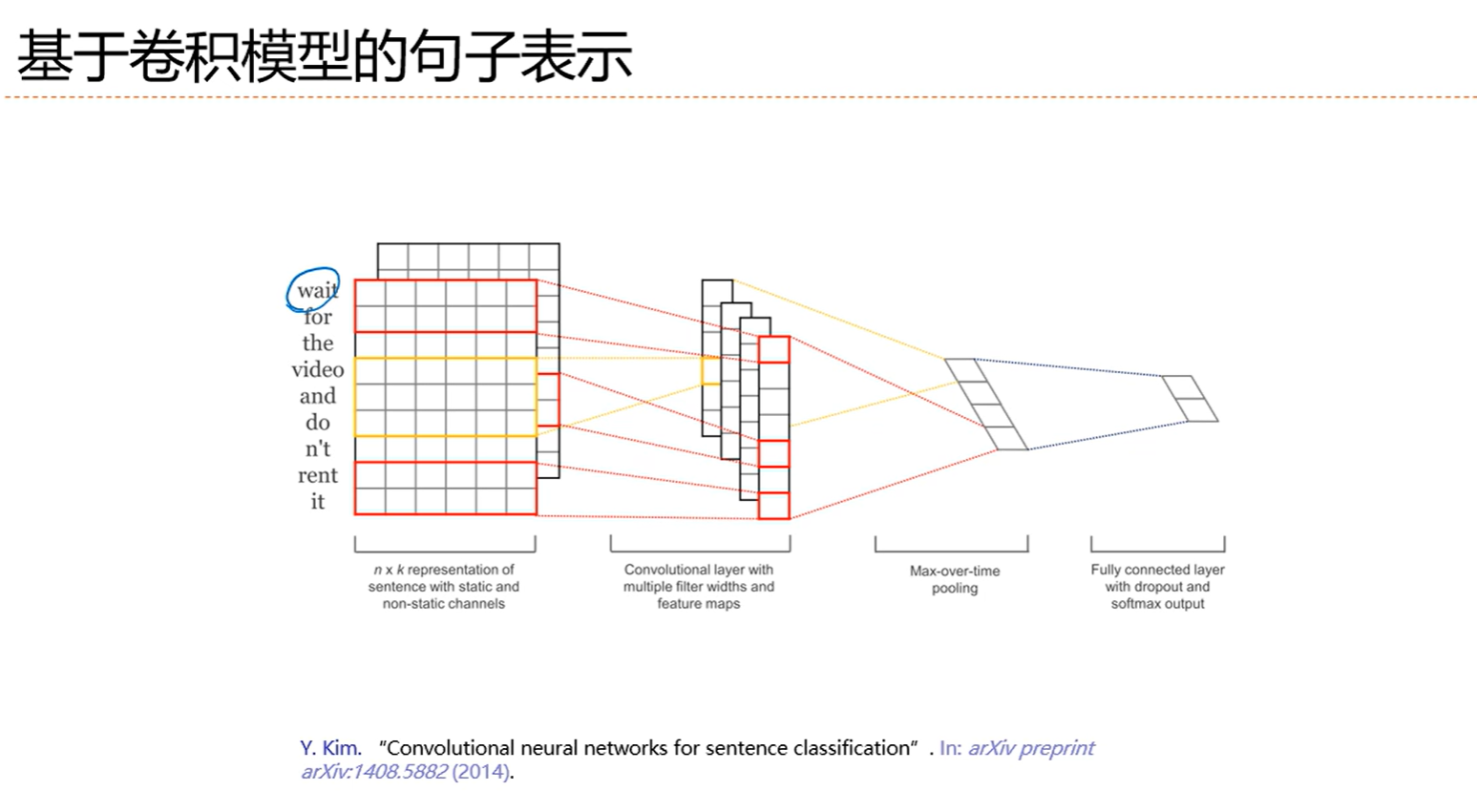
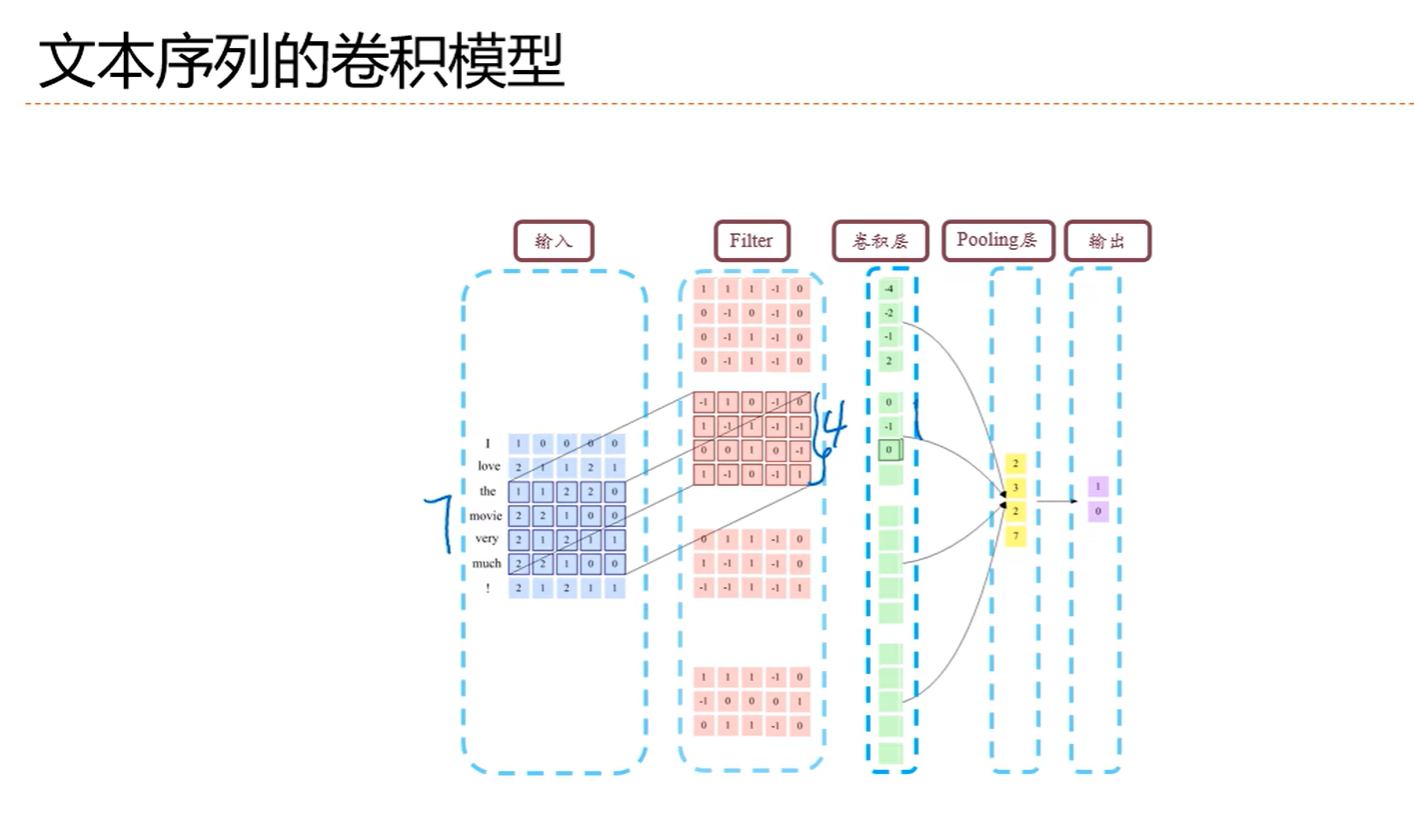
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Darlingの妙妙屋!
评论











