无符号数和有符号数加减法溢出判断及标志位变化

根据指令类型设置标志：
- 加法：CF = 最高位进位
- 减法：CF = 最高位进位取反
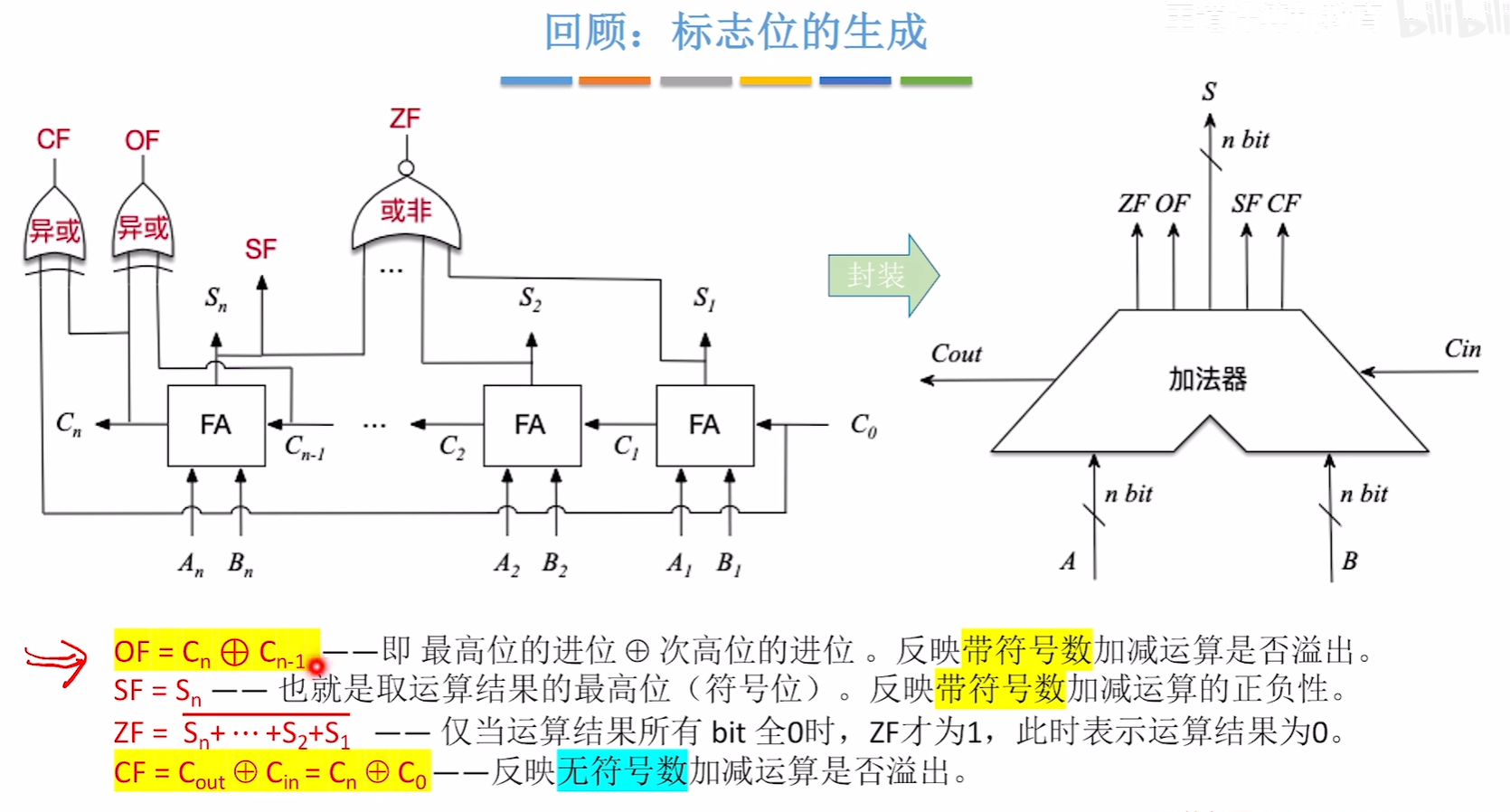
- OF：始终为 OF = 最高位进位 ⊕ 次高位进位

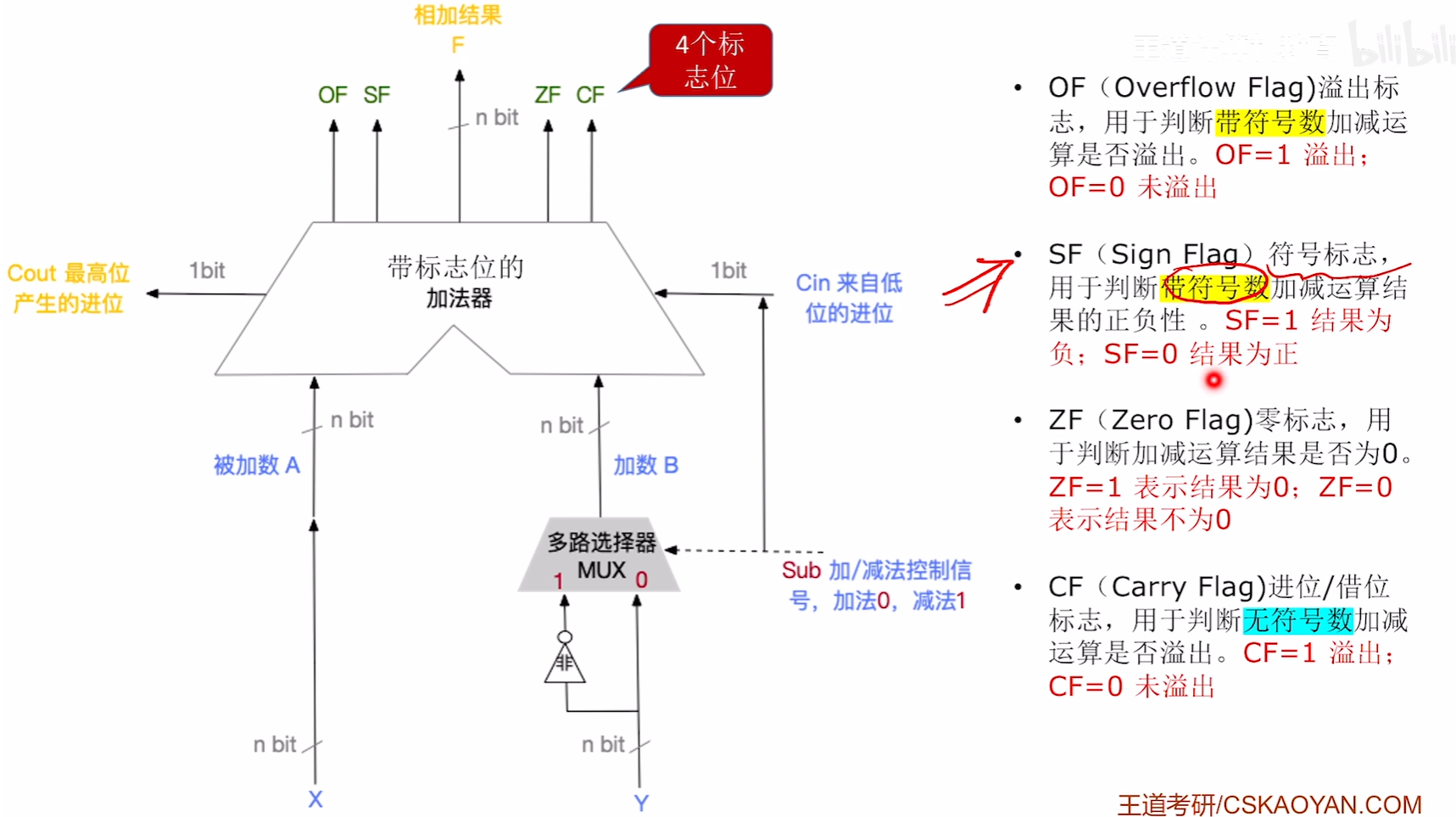
1.无符号数

1.溢出判断

加法：当结果超过n位能表示的最大值（2ⁿ-1）时，会发生进位，通过CF标志反映

减法：当被减数小于减数时，结果会小于0，发生借位，通过CF标志反映

如果溢出了，那么CF就是1

2.CF

加法规则：

当最高位产生进位时，CF=1
当最高位没有进位时，CF=0

减法规则（A - B）：

硬件执行 A + (~B + 1)（即加B的补码）
CF = NOT(加法最高位进位)
- 若加法最高位进位=1 → CF=0（无借位，不溢出）
- 若加法最高位进位=0 → CF=1（有借位，溢出）
简单记忆：CF=1表示有借位（A < B）

3.OF

OF = 最高位进位 ⊕ 次高位进位

最高位进位：符号位向更高位的进位
次高位进位：次高位向符号位的进位

1. 无符号加法

硬件执行两个无符号数相加，同时按有符号溢出规则计算OF：

将两个操作数当作有符号数（补码）解释
按照有符号溢出判断规则设置OF
OF=1 表示：如果这两个数是有符号数，加法会溢出
OF=0 表示：如果这两个数是有符号数，加法不会溢出

2. 无符号减法

硬件执行A - B，转换为A + (~B + 1)：

将A和-B当作有符号数解释
按照有符号溢出判断规则设置OF
OF=1 表示：如果这个减法在有符号解释下会溢出
OF=0 表示：如果这个减法在有符号解释下不会溢出

2.有符号数

1.溢出判断

2.1 溢出判断

n位有符号数（补码）范围：-2ⁿ⁻¹ ~ 2ⁿ⁻¹-1
加法溢出判断：

正数 + 正数 = 负数 → 上溢
负数 + 负数 = 正数 → 下溢
正数 + 负数 → 不会溢出

减法溢出判断（A - B）：

转换为 A + (-B) 后，按加法规则判断
正数 - 负数（即正数+正数）可能上溢
负数 - 正数（即负数+负数）可能下溢

2.CF

硬件设置CF的规则，与操作数是否被解释为有符号数无关，完全按照无符号运算的物理过程进行。

规则：

有符号加法：
- 硬件执行二进制位相加
- 如果最高位产生进位，则 CF = 1
- 否则 CF = 0
有符号减法（A - B）：
- 硬件转换为执行 A + (~B + 1)
- 如果这个加法运算的最高位产生进位，则 CF = 0（表示无借位）
- 如果这个加法运算的最高位未产生进位，则 CF = 1（表示有借位）
- 即：CF = NOT(加法最高位进位)

例子说明：A=FFFFFFFFH, B=FFFFFFF0H，计算A-B

硬件执行过程：

A:   1111 1111 1111 1111 1111 1111 1111 1111
-B:  0000 0000 0000 0000 0000 0000 0001 0000  （~B + 1 的结果）
-------------------------------------------------
    10000 0000 0000 0000 0000 0000 0000 1111
      ↑
      第31位向第32位的进位 = 1

CF值确定：