Day53 | 单调栈：接雨水&&柱形图中最大的矩形

单调栈【基础算法精讲 26】_哔哩哔哩_bilibili

42.接雨水

42. 接雨水 - 力扣（LeetCode）

image-20241205114540833

思路：

还是和昨天差不多一样的思路，只是昨天找到下一个更大元素就只是记录了一下，这次我们要用这个更大元素计算一下可以接多少雨水。

单调栈依旧是单调递减的，如图中所示。

我们要如何计算可以接多少雨水呢?

比如我们选定2,1,0,4这几个柱子

那就是先算1,0,4。

宽为4的下标减去1的下标再减1，高为1和4的最小值减去中间的0，宽*高即为答案，为1

再算2,1,4。

宽为4的下标减去2的下标再减1，高为2和4的最小值减去中间的1，宽*高即为答案，为2

再把两者相加就是2,1,0,4这几个柱子可以接多少雨水了

单调栈的入栈出栈过程：

灵神总结为：找上一个更大元素，在找的过程中填坑，我来举个例子大家就明白了。

5，入栈

2<5，入栈

1<2，入栈

0<1，入栈

4>0，我们找到了一个更大的元素

那就是计算以0为中心的柱子1,0,4可以接多少，然后把0弹出

计算以1为中心的柱子2,1,4可以接多少，然后把1弹出

计算以2为中心的柱子5,2,4可以接多少，然后把2弹出

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> st;
        int res=0;
        for(int i=0;i<height.size();i++)
        {
            while(!st.empty()&&height[i]>height[st.top()])
            {
                int mid=st.top();
                st.pop();
                if(st.empty())
                    break;
                int left=st.top();
                res=res+(i-left-1)*(min(height[i],height[left])-height[mid]);
                //          宽                  高
            }
            st.push(i);
        }
        return res;
    }
};

84.柱状图中的最大矩形

84. 柱状图中最大的矩形 - 力扣（LeetCode）

思路：

这次的单调栈是递增的

还是和接雨水一样，只是接雨水是中间凹下去的，比如1,0,4，中间的0要小于1和4

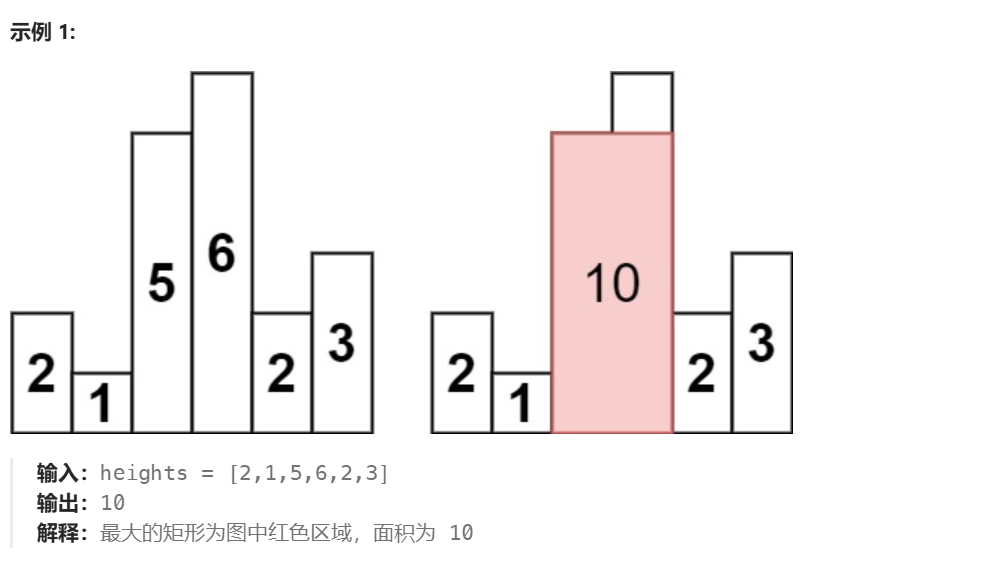
而这道题中间是突出来的，比如下图中的1，5，6，2，并且两边的柱子不能参与合并（就和上一题1,4不能接雨水一样）

即1,5,6,2中只有5,6可以去合并，如果是5,6,2的话那就是只有6了

如果碰到元素小于栈顶元素，我们才会去计算矩形的面积，否则不会计算

栈的具体过程：

那1,5,6,2举例

栈中为1,1<5,5入栈

5<6,6入栈

6>2，开始计算矩形大小

1
2
heights[i]=2;
heights[st.top()]=6;

到这里我们发现还需要栈顶元素的下一个元素5，才能够进行计算

1
2
3
4
5
st.pop();
heights[st.pop()]=5;
高：6
宽：i-st.top()-1=1;
最大矩形:6*1=6

继续，此时栈内为1,5，而heights[i]还是2，heights[st.pop()]就是5;

我们还是需要栈顶元素的下一个元素1，才能够进行计算

1
2
3
4
5
st.pop();
heights[st.pop()]=1;
高：5
宽：i-st.top()-1=2;
最大矩形:5*2=10

难理解的点：为什么要在数组前后多加高度为0的柱子?

第一根柱子和最后一根柱子如果是最高的，并且也没有多加高度为0的柱子的话，那是不会被计算的

如果heights为100,1那最后的结果还是0，因为我们没有进行任何的计算（栈顶为100，heights[i]为1，但是我们获取不到栈顶元素的下一个元素），但实际上应该是100

如果是1,100，栈顶为1，heights[i]为100，没有末尾的0，我们不会进行任何计算，因为它本身就是单调递增的

image-20241205120328724

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        // 在高度数组的两端添加 0
        heights.insert(heights.begin(), 0);
        heights.push_back(0);
        stack<int> s;
        int ans = 0;
        for (int i = 0; i < heights.size(); ++i) {
            while (!s.empty() && heights[i] < heights[s.top()]) {
                // 弹出栈顶，计算对应的面积
                int dh = heights[s.top()];
                s.pop();
                int dw = i - s.top() - 1;
                ans = max(ans, dh * dw);
            }
            // 将当前元素下标压入栈
            s.push(i);
        }
        return ans;
    }
};