Day55 | 灵神 | 相向双指针：盛最多水的容器&&接雨水

11.盛最多水的容器

这道题就不太能想到思路了（悲）

思路：

还是使用相向双指针

我们随便挑两根柱子，就比如图中的两根，左边的下标为l，右边的下标为r，那么能接的水就是

1	sum=min(height[l],height[r])*(r-l)

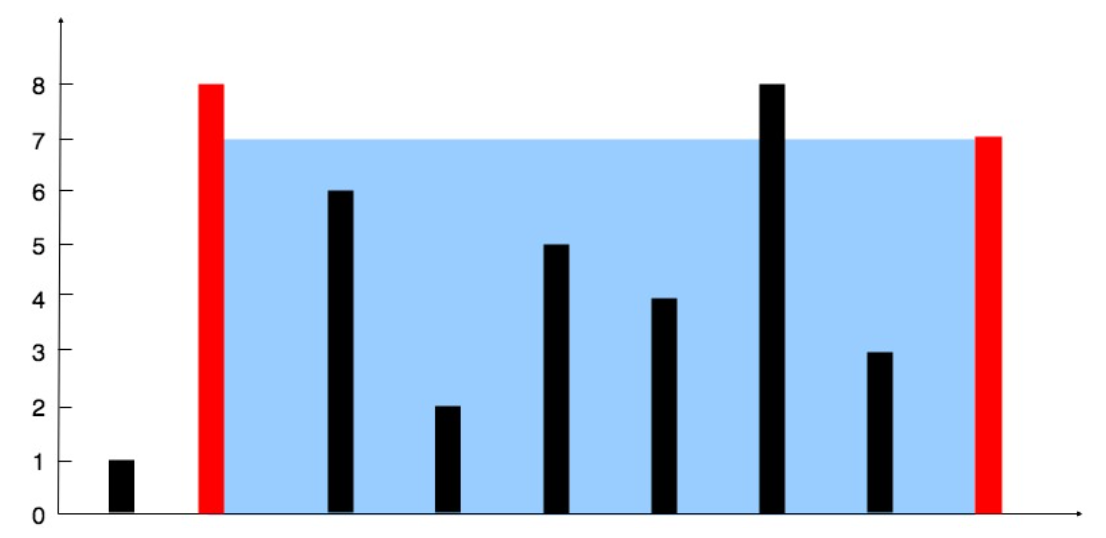
首先先找出短的一端，然后固定它，（为什么找短端而不找长端？这个稍后解释）这个例子中r比较短，那么就固定r。此时接水总量为

1	sum1=height[r]*(r-l)

分类讨论:

1.假设在l和r中间，找到一根比height[r]要小的柱子k来当左端

1	sum2=height[k]*(r-k)

由于

1 2	height[r]>height[k] r-l>r-k (因为k在l和r中间)

所以

sum1>sum2

就是说，高变小了，宽也变小了，那肯定比原来小了

2.假设在l和r中间，找到一根比height[r]要大的柱子i来当左端

1	sum3=height[r]*(r-i)

由于

1	r-i>r-l (因为i在l和r中间)

所以

sum1>sum3

这种是高没变，宽变小了，也肯定比原来小了

3.假设在l和r中间，找到一根和height[r]一样大的柱子j来当左端

那不用说了，高没变宽变小了，自然是不如l和r的大

综上所述，我们发现，图中l和r中间的柱子无论怎么取，都不如l和r的大。

可我们还要继续往遍历去找更大的值，去尝试得到更多的水，那该怎么继续遍历呢？

答案是移动短端，相当于去掉短的一端，看l和r-1这两根柱子。

因为我们发现了，只要固定住短端，长端只要在（l,r）中间取值，那都不可能比l和r大，所以这时候就只能移动短端了，就相当于把r给去掉了，去比较l和r-1，看看在这个区间里面有没有比在(l,r)的最大值更大的。

那结论就出来了，我们每次更新完最大值以后，就把短端给去掉即可。

完整代码：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int res=0;
        int l=0,r=height.size()-1;
        while(l<r)
        {
            //更新最大值
            int tmp=min(height[l],height[r])*(r-l);
            res=max(res,tmp);
            //去掉短端
            if(height[l]<height[r])
                l++;
            else    
                r--;
        }
        return res;
    }
};

看到这里你应该明白为什么找短端而不找长端，我们固定的是短端，这是因为算高度的时候看的是短端而不是长端，固定短端可以减少一个变量。

42.接雨水

42. 接雨水 - 力扣（LeetCode）

理解不了的话记个单调栈的做法也行。

思路：前后缀分解

笔者说个大概，如果看不懂的话可以去看灵神的视频。

怎么算：我们分别算出每一个柱子能接多少水，然后都加起来就是全部的

前缀就是包含当前柱子在内，当前柱子的前面最高的柱子高度

后缀就是包含当前柱子在内，当前柱子的后面最高的柱子高度

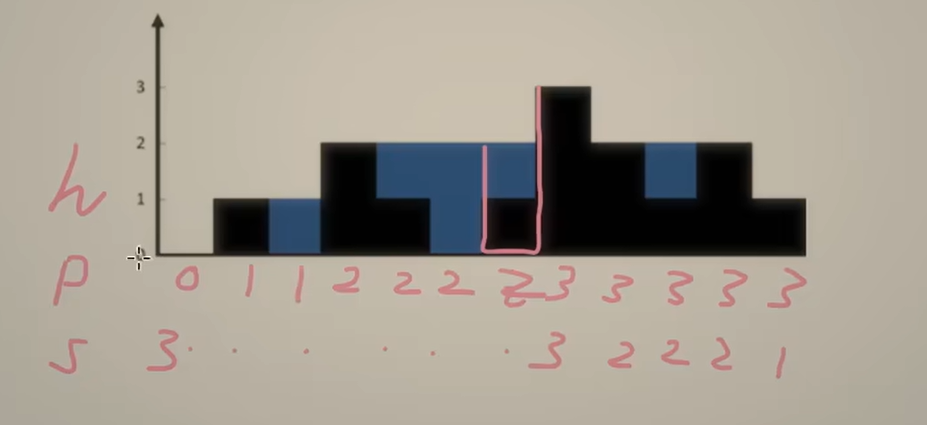
如图，上面一行是前缀，下面一行是后缀

就拿图中的第5列（下标为4）的柱子来举例子吧

它的前缀最大是2，后缀最大是3，那么如果只看它这一根柱子的话，它能接多少水就是，前缀和后缀选个小的（大的柱子比小的柱子多的部分装不了水），再减去柱子本身的高度

对于第5列就是 min(3,2)-1=1，所以这根柱子可以接1格水

其他柱子都这么算一遍然后把每个柱子的水加起来就是答案了

完整代码：

class Solution {
public:
    int trap(vector<int>& height) {
        int mpre=0,mtail=0;
        vector<int> pre(height.size(),0);
        vector<int> tail(height.size(),0);
        //计算前缀
        for(int i=0;i<height.size();i++)
        {
            mpre=max(mpre,height[i]);
            pre[i]=mpre;
        }
        //计算后缀
        for(int i=height.size()-1;i>=0;i--)
        {
            mtail=max(mtail,height[i]);
            tail[i]=mtail;
        }
        //计算每个柱子的水
        int res=0;
        for(int i=0;i<height.size();i++)
            res+=(min(tail[i],pre[i])-height[i]);
        return res;
    }
};

优化：双指针做法

这个好难用文字讲出来，大家听灵神的视频讲解吧

总体思路还是一个柱子一个柱子算，算完一个再算下一个

class Solution {
public:
    int trap(vector<int>& height) {
        int r=height.size()-1,l=0;
        //分别保存前缀和后缀的两个值
        int mpre=height[l],mtail=height[r];
        int res=0;
        while(l<r)
        {
            //前缀小于后缀
            //那计算当前柱子能接多少水就取决于前缀了，因为比前缀多的部分就流走了
            if(mpre<mtail)
            {
                //计算能接多少水
                res+=mpre-height[l];
                //计算完当前柱子可以接多少水就去算下一个柱子
                l++;
                //更新前缀的值
                mpre=max(mpre,height[l]);
            }
            //前缀大于后缀
            //那计算当前柱子能接多少水就取决于后缀了，因为比后缀多的部分就流走了
            else
            {
                //计算能接多少水
                res+=mtail-height[r];
                //计算完当前柱子可以接多少水就去算下一个柱子
                r--;
                //更新后缀的值
                mtail=max(mtail,height[r]);
            }
        }
        return res;
    }
};